题目内容
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 上的最值;
上的最值;
(2)设![]() ,若当
,若当![]() ,且
,且![]() 时,
时,![]() ,求整数
,求整数![]() 的最小值..
的最小值..
【答案】(1)详见解析(2)2
【解析】
(1)先对函数求导,然后讨论参数![]() 的范围,分别判断每种情况下
的范围,分别判断每种情况下![]() 的单调性,即可求出对应的最值;
的单调性,即可求出对应的最值;
(2)先写出![]() 的解析式,分两种情况讨论:
的解析式,分两种情况讨论:
当![]() 时,由(1)易知
时,由(1)易知![]() 时,
时,![]() ,从而
,从而![]() ,进而可得m的范围;
,进而可得m的范围;
当![]() 时,可将
时,可将![]() 变形为
变形为![]() ,只需用导数的方法研究
,只需用导数的方法研究![]() 的单调性和最值即可;
的单调性和最值即可;
解法一:
(1)![]() ,
,
①当![]() 时,
时,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,无最小值.
,无最小值.
②当![]() 时,
时,
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
令![]() ,解得
,解得![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
所以![]() ,无最大值.
,无最大值.
③当![]() 时,
时,
因为![]() ,等号仅在
,等号仅在![]() ,
,![]() 时成立,
时成立,
所以![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,无最大值.
,无最大值.
综上,当![]() 时,
时,![]() ,无最小值;当
,无最小值;当![]() 时,
时,![]() ,无最大值;当
,无最大值;当![]() 时,
时,![]() ,无最大值.
,无最大值.
(2)![]() ,
,
当![]() 时,因
时,因![]() 为,由(1)知
为,由(1)知![]() ,所以
,所以![]() (当
(当![]() 时等号成立),所以
时等号成立),所以![]() .
.
当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化为
,已知化为![]() 在
在![]() 上恒成立,
上恒成立,
因为![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
又因为![]() ,
,![]() ,
,
所以存在![]() 使得
使得![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() 的最小整数值为2.
的最小整数值为2.
解法二:
(1)同解法一.
(2)![]() ,
,
①当![]() 时,因
时,因![]() 为,由(1)知
为,由(1)知![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
②当![]() 时,因为
时,因为![]() ,
,![]() ,所以
,所以![]() ,
,
令![]() ,
,![]() ,已知化为
,已知化为![]() 在
在![]() 上恒成立,
上恒成立,
因为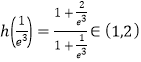 在
在![]() 上,所以
上,所以![]() ,
,
下面证明![]() ,即证
,即证![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,![]() ,
,
则![]() ,令
,令![]() ,得,
,得,
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递减;
上递减;
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上递增,
上递增,
所以![]() ,且
,且![]() ,
,
所以当![]() 时,
时,![]() ,即
,即![]() .
.
由①②得当![]() 时,
时,![]() ,
,
所以![]() 的最小整数值为2.
的最小整数值为2.

【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.

