题目内容
3.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,若D,E分别在BC,BA上,且$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$\overrightarrow{BE}$=2$\overrightarrow{EA}$,则向量$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$表示( )| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{CE}$ | C. | $\overrightarrow{DE}$ | D. | $\overrightarrow{ED}$ |
分析 根据条件作出图形,并在边AC上取点F,使得AF=$\frac{2}{3}AC$,然后连接DE,DF,AD,可以说明四边形AEDF为平行四边形,从而根据向量加法的平行四边形法则即可得出$\frac{2}{3}\overrightarrow{b}+\frac{1}{3}\overrightarrow{c}=\overrightarrow{AF}+\overrightarrow{AE}=\overrightarrow{AD}$.
解答 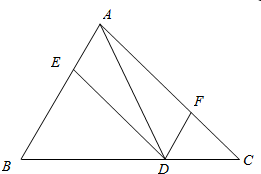 解:如图,$\overrightarrow{BD}=2\overrightarrow{DC},\overrightarrow{BE}=2\overrightarrow{EA}$;
解:如图,$\overrightarrow{BD}=2\overrightarrow{DC},\overrightarrow{BE}=2\overrightarrow{EA}$;
∴$CD=\frac{1}{3}BC,AE=\frac{1}{3}AB$;
在AC上取F,使$AF=\frac{2}{3}AC$;
∴$CF=\frac{1}{3}AC$;
∴DF∥AB,DF=$\frac{1}{3}AB=AE$;
即DF∥AE,且DF=AE;
连接DE,DF,AD,则四边形AEDF为平行四边形;
∴$\frac{2}{3}\overrightarrow{b}+\frac{1}{3}\overrightarrow{c}=\frac{2}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{AB}$=$\overrightarrow{AF}+\overrightarrow{AE}=\overrightarrow{AD}$.
故选:A.
点评 考查向量数乘的几何意义,平行线分线段成比例,平行四边形的判定,以及向量加法的平行四边形法则.

练习册系列答案
相关题目
13.已知Sn为数列{an}的前n项和,且满足a1=1,a2=3,an+2=3an+1,则S2014=( )
| A. | 2×31007-2 | B. | 2×31007 | C. | $\frac{{3}^{2014}-1}{2}$ | D. | $\frac{{3}^{2014}+1}{2}$ |
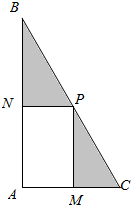 某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].
某中学为了落实“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上,已知∠ACB=60°且|AC|=30米,|AM|=x米,x∈[10,20].