题目内容
11.研究函数y=sin|x|的性质(定义域、值域、周期、奇偶性、单调性、最值).分析 对于函数y=sin|x|,画出它的图象,数形结合可得揭露.
解答 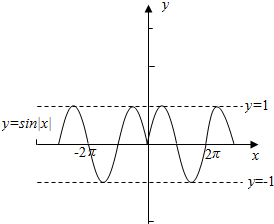 解:对于函数y=sin|x|,画出它的图象,如图所示:
解:对于函数y=sin|x|,画出它的图象,如图所示:
数形结合可得
它的定义域为R,值域为[-1,1],没有周期性,它是偶函数.
当x>0时,它的增区间为[0,$\frac{π}{2}$]、[2kπ+$\frac{3π}{2}$,2kπ+$\frac{5π}{2}$]k∈N;
减区间为[2kπ+$\frac{π}{2}$,2kπ+$\frac{3π}{2}$]k∈N.
当x<0时,它的增区间为[2kπ-$\frac{3π}{2}$,2kπ-$\frac{π}{2}$],k∈Z;
它的减区间为[-$\frac{π}{2}$,0],[2k-$\frac{5π}{2}$,2kπ-$\frac{3π}{2}$],k∈Z.
它的最大值为1,最小值为-1.
点评 本题主要考查正弦函数的图象特征,正弦函数的性质,体现了数形结合的数学思想,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.函数y=tan($\frac{π}{3}$-x)的定义域是( )
| A. | {x|x∈R,且x≠-$\frac{π}{3}$} | B. | {x|x∈R,且x≠$\frac{5}{6}π$} | ||
| C. | {x|x∈R,且x≠kπ+$\frac{5}{6}$π,k∈Z} | D. | {x|x∈R,且x≠kπ-$\frac{5}{6}$π,k∈Z} |
3.在△ABC中,$\overrightarrow{AB}$=$\overrightarrow{c}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,若D,E分别在BC,BA上,且$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$\overrightarrow{BE}$=2$\overrightarrow{EA}$,则向量$\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$表示( )
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{CE}$ | C. | $\overrightarrow{DE}$ | D. | $\overrightarrow{ED}$ |