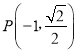Question

【题目】有一种类型的题目，此类题目有六个选项A、B、C、D、E、F，其中有三个正确选项，满分6分，赋分标准为“每选对一个得2分，每选错一个扣3分，最低得分为0分”.在某校的一次测试中出现了这种类型的题目，已知此题的正确答案是A、C、D，假定考生作答的答案中选项的个数不超过三个.

（1）若甲同学只能判断选项A、D是正确的，现在他有两种选择：一种是将A、D作为答案，另一种是在B、C、E、F这四个选项中任选一个与A、D组成一个含三个选项的答案.则甲同学的最佳选择是哪一种？请说明理由；

（2）若乙同学无法判断所有选项，他决定在6个选项中任选3个作为答案：

（i）设乙同学此题得分为分，求的分布列；

（ii）已知有20名和乙同学情况相同的同学，且这20名考生答案互不相同，他们此题的平均得分为a分，现从这20名考生中任选3名考生，计算得到这3人平均得分为b分，试求a的值及的概率.

Answer 1

【答案】（1）甲同学最佳选择是选，理由见解析；（2）（ⅰ）分布列见解析，（ⅱ）

【解析】

（1）分别计算两种情况的得分的数学期望，从而可做出结论；

（2）（i）写出的所有可能取值，分别计算概率即可；

（ii）由（i）的分布列可求a，再计算出的概率，从而可求的概率.

（1）设甲同学此题得分为X，

①若甲同学选择，则，X的数学期望；

②若甲同学选择3个选项，则其答案共种.其中得分为1分的情况有种情况，其概率为，得分为6分的情况有1种，其概率为，所以X的数学期望，

故甲同学最佳选择是选.

（2）（i）乙同学可能的答案共种.其中得分为6分的情况有1种，概率为，

得分为1分的情况有种，概率为，

得分为0分的概率为，

故可取0，1，6，且，，，所以的分布列为：

	0	1	6
P

（ii）由（i）可知.

由于这20名考生的答案互不相同且可能的答案总数为20，因此这20名考生有10人的得分均为0分，9人的得分均为1分，1人的得分为6分.

则当时任选的3名考生的得分有3种情况符合要求：分别为0分，0分，0分或0分，0分，1分或0分，1分，1分，即任选的3名考生中3人得0分，或2人得0分，1人得1分，或1人得0分，2人得1分.

所以.

∴的概率为：.