Question

【题目】试研究，一个三角形能否同时具有以下两个性质：（1）三边是连续的三个自然数；（2）最大角是最小角的2倍.若能，请求出这个三角形的三边以及最大角的余弦值；若不能，请说明理由.

Answer 1

【答案】4，5，6；最大角的余弦值为．

【解析】

设三角形的三边分别为，，，对应的角分别为，则，由正弦定理及二倍角的正弦公式可得，又由余弦定理得，则，解出方程即可求出三边，再根据余弦定理即可求出最大角的余弦值．

解：设三角形的三边分别为，，，对应的角分别为，

则，由题意可得，

由正弦定理可得，

∴，

又由余弦定理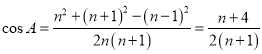可得，

∴，化简可得，解得，或（舍去），

∴三角形的三边分别为4，5，6，

∴三角形的最大角的余弦值，

综上：存在三角形的三边分别为4，5，6满足题意，最大角的余弦值为．