题目内容
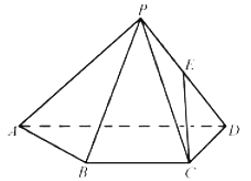
【题目】如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(I)证明:CE∥平面PAB;
(II)求直线CE与平面PBC所成角的正弦值
【答案】(I)见解析;(II)![]() .
.
【解析】试题本题主要考查空间点、线、面位置关系,直线与平面所成的角等基础知识,同时考查空间想象能力和运算求解能力。满分15分。
(Ⅰ)取PA中点F,构造平行四边形BCEF,可证明;(Ⅱ)由题意,取BC,AD的中点M,N,可得AD⊥平面PBN,即BC⊥平面PBN,过点Q作PB的垂线,垂足为H,连结MH.可知MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.依此可在Rt△MQH中,求∠QMH的正弦值.
试题解析:
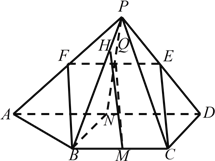
(Ⅰ)如图,设PA中点为F,连接EF,FB.
因为E,F分别为PD,PA中点,所以![]() 且
且![]() ,
,
又因为![]() ,
, ![]() ,所以
,所以![]() 且
且![]() ,
,
即四边形BCEF为平行四边形,所以![]() ,
,
因此![]() 平面PAB.
平面PAB.
(Ⅱ)分别取BC,AD的中点为M,N.连接PN交EF于点Q,连接MQ.
因为E,F,N分别是PD,PA,AD的中点,所以Q为EF中点,
在平行四边形BCEF中,MQ//CE.
由△PAD为等腰直角三角形得PN⊥AD.
由DC⊥AD,N是AD的中点得BN⊥AD.
所以AD⊥平面PBN,
由BC//AD得BC⊥平面PBN,
那么平面PBC⊥平面PBN.
过点Q作PB的垂线,垂足为H,连接MH.
MH是MQ在平面PBC上的射影,所以∠QMH是直线CE与平面PBC所成的角.
设CD=1.
在△PCD中,由PC=2,CD=1,PD=![]() 得CE=
得CE=![]() ,
,
在△PBN中,由PN=BN=1,PB=![]() 得QH=
得QH=![]() ,
,
在Rt△MQH中,QH=![]() ,MQ=
,MQ=![]() ,
,
所以sin∠QMH=![]() ,
,
所以直线CE与平面PBC所成角的正弦值是![]() .
.

【题目】2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 4 | 36 | 96 | 28 | 32 | 4 |
(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损 100元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |

【题目】据统计,某地区植被覆盖面积![]() 公顷
公顷![]() 与当地气温下降的度数
与当地气温下降的度数![]() 之间呈线性相关关系,对应数据如下:
之间呈线性相关关系,对应数据如下:
| 20 | 40 | 60 | 80 |
| 3 | 4 | 4 | 5 |
![]() 请用最小二乘法求出y关于x的线性回归方程;
请用最小二乘法求出y关于x的线性回归方程;
![]() 根据
根据![]() 中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少
中所求线性回归方程,如果植被覆盖面积为300公顷,那么下降的气温大约是多少![]() ?
?
参考公式:线性回归方程![]() ;其中
;其中![]() ,
,![]() .
.