题目内容
【题目】在![]() 点测量到远处有一物体在做匀速直线运动,开始时该物体位于点
点测量到远处有一物体在做匀速直线运动,开始时该物体位于点![]() ,一分钟后,其位置在
,一分钟后,其位置在![]() 点,且
点,且![]() ,再过二分钟后,该物体位于
,再过二分钟后,该物体位于![]() 点,且
点,且![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.以上均不正确
D.以上均不正确
【答案】C
【解析】
由题意可设PQ=x,则QR=2x,结合已知可表示∠R=30°﹣∠OPQ,在△ORQ中,△OPQ中分别利用正弦定理![]() ,OQ=
,OQ=![]() 表示OQ,变形整理,进而可得解.
表示OQ,变形整理,进而可得解.
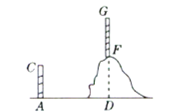
如下图所示,物体位于点P,一分钟后,其位置在Q点,再过二分钟后,该物体位于R点

∴设PQ=x,则QR=2x,
又∵∠POQ=90°,∠QOR=60°
∠OPQ+∠R=30°,即∠R=30°﹣∠OPQ
在△ORQ中,由正弦定理得![]()
OQ=![]() 在△OPQ中,由正弦定理得OQ=
在△OPQ中,由正弦定理得OQ=![]() =xsin∠OPQ∴
=xsin∠OPQ∴![]()
整理可得,![]()
![]() ,
,![]() .
.
故选C.

练习册系列答案
相关题目
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.