题目内容
正方体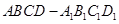 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.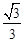 | C. | D.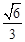 |
D
解析试题分析:根据题意,可以借助于体积法的得到点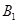 到平面的距离,因为
到平面的距离,因为 与平面
与平面 所成角,等于
所成角,等于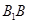 与平面
与平面 所成角,那么根据底面是等腰三角形,设正方体的边长为1,可知其面积为
所成角,那么根据底面是等腰三角形,设正方体的边长为1,可知其面积为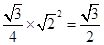 ,即根据
,即根据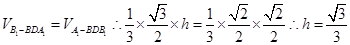
而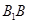 =1,则线面角的正弦值为
=1,则线面角的正弦值为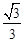 ,而其余弦值为
,而其余弦值为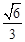 ,选D.
,选D.
考点:本试题考查了线面角的求解运用。
点评:解决线面角的求解,关键是作出角,利用平面的垂线,和斜线在平面内的射影,结合斜线段和斜线段在平面内的射影的夹角来得到结论,或者利用斜线段和垂线段的长度比值来得到。属于基础题。

练习册系列答案
相关题目
如图是一个正三棱柱体的三视图,该柱体的体积等于
A. | B.2 | C.2 | D. |
如图,在正方体 中,点
中,点 在线段
在线段 上移动,则异面直线
上移动,则异面直线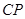 与
与 所成的角
所成的角 的取值范围( )
的取值范围( )
A. | B. |
C. | D. |
一空间几何体的三视图如图,则该几何体的体积为( ) 
A.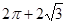 | B.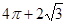 |
C. | D.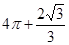 |
下列说法正确的是( )
| A.空间三个点确定一个平面 | B.两个平面一定将空间分成四部分 |
| C.梯形一定是平面图形 | D.两个平面有不在同一条直线上的三个交点 |
 ,则球的表面积( )
,则球的表面积( ) B、
B、 C、
C、 D、
D、
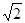
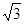




 ,∠ASC=∠BSC=30°,则棱锥SABC的体积为( )
,∠ASC=∠BSC=30°,则棱锥SABC的体积为( )