题目内容
已知球的半径为2,相互垂直的两个平面分别截球面得两个圆,若两圆的公共弦长为2,则两圆的圆心距等于( )
| A.1 | B.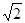 | C.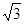 | D.2 |
C
解析试题分析:设球心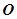 两截面小圆圆心到
两截面小圆圆心到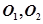 公共弦的中点为
公共弦的中点为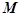 ,由圆中的性质可知四边形
,由圆中的性质可知四边形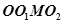 为矩形,
为矩形,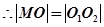 ,由弦长一半,球的半径,球心到弦中点的线段构成直角三角形可知
,由弦长一半,球的半径,球心到弦中点的线段构成直角三角形可知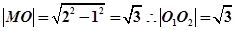
考点:球的截面圆问题
点评:一平面去截球,截面小圆半径,球心到小圆的距离,球的半径构成直角三角形

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
已知球的直径SC=4,A,B是该球球面上的两点,AB=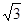 ,
,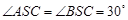 ,则棱锥S—ABC的体积为( )
,则棱锥S—ABC的体积为( )
A. | B.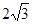 | C.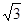 | D.1 |
正方体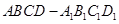 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.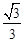 | C. | D.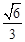 |
若轴截面为正方形的圆柱的侧面积是 ,那么圆柱的体积等于
,那么圆柱的体积等于
A. | B. | C. | D. |
一个几何体的三视图及其尺寸(单位:cm) ,如图所示,则该几何体的体积为( ) .
. 
| A.144 | B.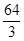 | C. | D.64 |
 的正方形,主视图与左视图是边长为
的正方形,主视图与左视图是边长为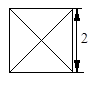




 ,AC=1,则A,B两点在三棱锥的外接球的球面上的距离为( )
,AC=1,则A,B两点在三棱锥的外接球的球面上的距离为( )





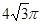


 的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为
的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为



