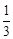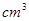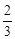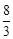题目内容
一空间几何体的三视图如图,则该几何体的体积为( ) 
A.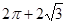 | B.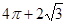 |
C. | D.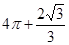 |
C
解析试题分析:由于根据三视图的特点可知,该几何体是一个简单的组合体,上面是四棱锥,下面是圆柱体,且棱锥的底面为正方形,边长为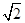 ,高为
,高为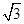 ,圆柱体的底面的半径为1,高位2,因此可知其体积为
,圆柱体的底面的半径为1,高位2,因此可知其体积为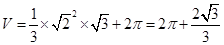 ,故选A.
,故选A.
考点:本试题考查了空间几何体体积的知识。
点评:根据已知的三视图,分析得到原几何体是一个四棱锥和一个圆柱体的组合体。进而结合柱体的体积公式和锥体的体积公式来求解得到。关键是弄清楚各个几何体的高度和底面的边长和圆的半径,属于中档题。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
正方体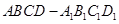 中,
中, 与平面
与平面 所成角的余弦值为( )
所成角的余弦值为( )
A. | B.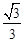 | C. | D.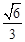 |
一空间几何体的三视图如图,则该几何体的体积为( )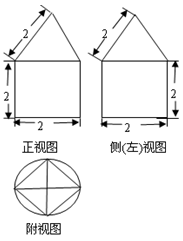
A.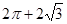 | B.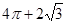 |
C.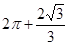 | D.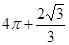 |
若轴截面为正方形的圆柱的侧面积是 ,那么圆柱的体积等于
,那么圆柱的体积等于
A. | B. | C. | D. |
把3个半径为R的铁球熔化铸成一个底面半径为R的圆柱(不计损耗),则圆柱的高为( )
A. | B.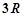 | C. | D.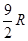 |
某几何体的三视图如下,则几何体的表面积为( )。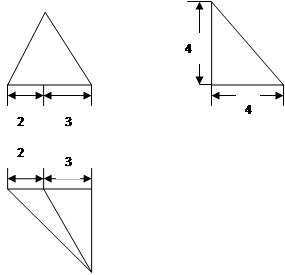
A.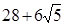 | B.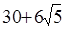 |
C.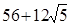 | D. |





 的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为
的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为




 ),则这个三棱锥的体积是
),则这个三棱锥的体积是