题目内容
【题目】(本小题共13分)已知函数![]()
![]() 的最小正周期为
的最小正周期为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调区间及其图象的对称轴方程.
的单调区间及其图象的对称轴方程.
【答案】解:(Ⅰ)![]() ………………………2分
………………………2分
![]() , …………………………3分
, …………………………3分
因为![]() 最小正周期为
最小正周期为![]() ,所以
,所以![]() ,解得
,解得![]() ,………………………4分
,………………………4分
所以![]() , …………………… 5分
, …………………… 5分
所以![]() . …………………………6分
. …………………………6分
(Ⅱ)分别由![]() ,
,![]()
可得![]() ,
,![]() ………8分
………8分
所以,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 的单调减区间为
的单调减区间为![]() ………………………10分
………………………10分
由![]() 得
得![]() .
.
所以,![]() 图象的对称轴方程为
图象的对称轴方程为![]() . ………………………13分
. ………………………13分
【解析】
试题(Ⅰ)![]()
![]() ,因为
,因为![]() 最小正周期为
最小正周期为![]() ,可得
,可得![]() , 可得
, 可得![]() ,即可求出
,即可求出![]() .(Ⅱ)分别由
.(Ⅱ)分别由![]() ,
,![]() 即可求出单调区间;再根据
即可求出单调区间;再根据![]() ,可得
,可得
![]() 图象的对称轴方程.
图象的对称轴方程.
试题解析:解:(Ⅰ)![]()
![]() ,
,
因为![]() 最小正周期为
最小正周期为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
所以![]() .
.
(Ⅱ)分别由![]() ,
,![]()
可得![]() ,
,![]()
所以,函数![]() 的单调增区间为
的单调增区间为![]() ;
;
![]() 的单调减区间为
的单调减区间为![]()
由![]() 得
得![]() .
.
所以,![]() 图象的对称轴方程为
图象的对称轴方程为![]() .
.

练习册系列答案
相关题目
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,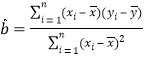
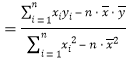 ,
,![]() .
.