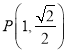题目内容
【题目】某公司生产的某种产品,如果年返修率不超过千分之一,则其生产部门当年考核优秀,现获得该公司2011-2018年的相关数据如下表所示:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年生产台数(万台) | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 |
该产品的年利润(百万元) | 2.1 | 2.75 | 3.5 | 3.25 | 3 | 4.9 | 6 | 6.5 |
年返修台数(台) | 21 | 22 | 28 | 65 | 80 | 65 | 84 | 88 |
部分计算结果:
| ||||||||
注:年返修率=![]()
(1)从该公司2011-2018年的相关数据中任意选取3年的数据,以![]() 表示3年中生产部门获得考核优秀的次数,求
表示3年中生产部门获得考核优秀的次数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)根据散点图发现2015年数据偏差较大,如果去掉该年的数据,试用剩下的数据求出年利润![]() (百万元)关于年生产台数
(百万元)关于年生产台数![]() (万台)的线性回归方程(精确到0.01).
(万台)的线性回归方程(精确到0.01).
附:线性回归方程![]() 中,
中,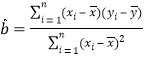
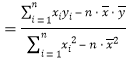 ,
,![]() .
.
【答案】(1)见解析;(2)![]()
【解析】
(1)先判断得到随机变量![]() 的所有可能取值,然后根据古典概型概率公式和组合数计算得到相应的概率,进而得到分布列和期望.(2)由于去掉
的所有可能取值,然后根据古典概型概率公式和组合数计算得到相应的概率,进而得到分布列和期望.(2)由于去掉![]() 年的数据后不影响
年的数据后不影响![]() 的值,可根据表中数据求出
的值,可根据表中数据求出![]() ;然后再根据去掉
;然后再根据去掉![]() 年的数据后所剩数据求出
年的数据后所剩数据求出![]() 即可得到回归直线方程.
即可得到回归直线方程.
(1)由数据可知,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五个年份考核优秀.
五个年份考核优秀.
由题意![]() 的所有可能取值为
的所有可能取值为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故![]() 的分布列为:
的分布列为:
|
|
|
|
|
|
|
|
|
|
所以![]() .
.
(2)因为![]() ,所以去掉
,所以去掉![]() 年的数据后不影响
年的数据后不影响![]() 的值,
的值,
所以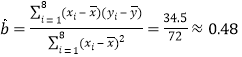 .
.
又去掉![]() 年的数据之后
年的数据之后![]() ,
,![]()
所以![]() ,
,
从而回归方程为:![]() .
.

练习册系列答案
相关题目