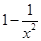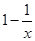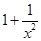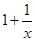题目内容
已知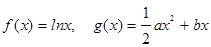
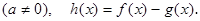
(1)当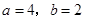 时,求
时,求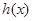 的极大值点;
的极大值点;
(2)设函数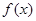 的图象
的图象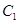 与函数
与函数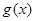 的图象
的图象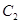 交于
交于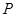 、
、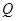 两点,过线段
两点,过线段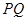 的中点做
的中点做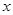 轴的垂线分别交
轴的垂线分别交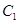 、
、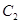 于点
于点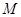 、
、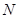 ,证明:
,证明: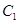 在点
在点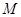 处的切线与
处的切线与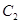 在点
在点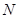 处的切线不平行.
处的切线不平行.
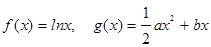
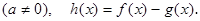
(1)当
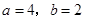 时,求
时,求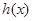 的极大值点;
的极大值点;(2)设函数
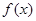 的图象
的图象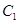 与函数
与函数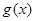 的图象
的图象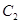 交于
交于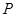 、
、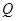 两点,过线段
两点,过线段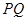 的中点做
的中点做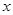 轴的垂线分别交
轴的垂线分别交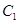 、
、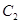 于点
于点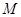 、
、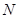 ,证明:
,证明: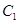 在点
在点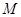 处的切线与
处的切线与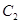 在点
在点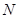 处的切线不平行.
处的切线不平行.(1)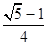 ;(2)证明见解析.
;(2)证明见解析.
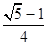 ;(2)证明见解析.
;(2)证明见解析.试题分析:(1)极值点的求法是利用导数知识求解,求出
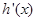 ,求得
,求得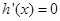 的解
的解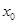 ,然后确定当
,然后确定当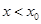 以及
以及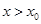 时的
时的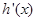 的符号,若当
的符号,若当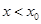 时,
时,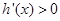 ,当
,当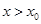 时,
时,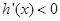 ,则
,则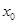 是极大值点,反之是极小值点;(2)题设中没有其他的已知条件,我们只能设
是极大值点,反之是极小值点;(2)题设中没有其他的已知条件,我们只能设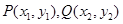
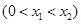 ,则
,则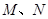 的横坐标为
的横坐标为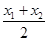 ,利用导数可得出切线的斜率
,利用导数可得出切线的斜率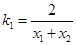 ,
,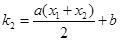 ,题设要证明的否定性命题,我们用反证法,假设两切线平行,即
,题设要证明的否定性命题,我们用反证法,假设两切线平行,即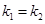 ,也即
,也即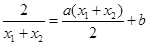 ,下面的变化特别重要,变化的意图是把这个等式与已知函数联系起来,等式两边同乘以
,下面的变化特别重要,变化的意图是把这个等式与已知函数联系起来,等式两边同乘以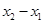 ,得
,得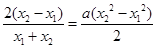
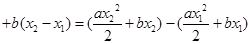
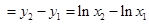
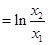 ,从而等式变为
,从而等式变为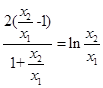 ,注意到
,注意到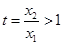 ,此等式为
,此等式为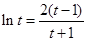 能否成立?能成立,说明存在平行,不能成立说明不能平行.设
能否成立?能成立,说明存在平行,不能成立说明不能平行.设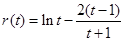 ,仍然用导数的知识来研究函数的性质,
,仍然用导数的知识来研究函数的性质,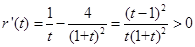 ,即
,即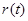 是增函数,从而在
是增函数,从而在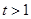 时,
时,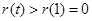 ,即等式
,即等式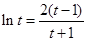 不可能成立,假设不成立,结论得证.
不可能成立,假设不成立,结论得证.试题解析:(1)

 2分
2分令h’(x)=0,则4x2+2x-1=0,
解出x1=
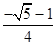 ,x2=
,x2=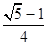 3分
3分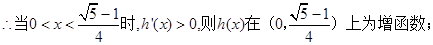 4分
4分 5分
5分所以
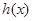 的极大值点为
的极大值点为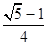 6分
6分(2)设P、Q的坐标分别是
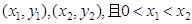 .
.则M、N的横坐标
 .
.∴C1在点M处的切线斜率为
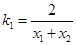 ,
,C2在点N处的切线斜率为
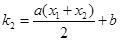 . 7分
. 7分假设C1在点M处的切线与C2在点N处的切线平行,则
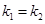 ,
,即
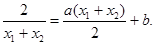 8分
8分则

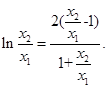 10分
10分设t=
 ,则
,则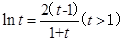 ①
①令
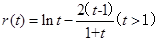 则
则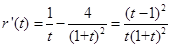
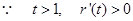
∴r(t)在[1,+∞)上单调递增,故r(t)>r(1)=0.
∴
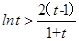 ,这与①矛盾,假设不成立,
,这与①矛盾,假设不成立,故C1在点M处的切线与C2在点N处的切线不平行. 12分

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
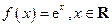 .
.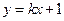 与
与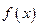 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值; ,讨论曲线
,讨论曲线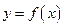 与曲线
与曲线 公共点的个数;
公共点的个数;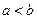 ,比较
,比较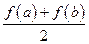 与
与 的大小,并说明理由.
的大小,并说明理由.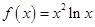 .
.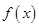 的单调区间;
的单调区间;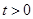 ,存在唯一的
,存在唯一的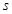 ,使
,使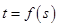 ;
;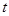 的函数为
的函数为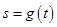 ,证明:当
,证明:当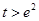 时,有
时,有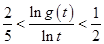 .
.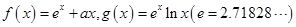 ..
..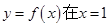 处的切线为
处的切线为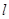 ,点(1,0)到直线l的距离为
,点(1,0)到直线l的距离为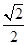 ,求a的值;
,求a的值;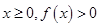 恒成立,试确定
恒成立,试确定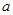 的取值范围;
的取值范围;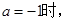 是否存在实数
是否存在实数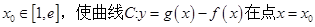 处的切线与y轴垂直?若存在,求出
处的切线与y轴垂直?若存在,求出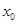 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.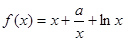 ,(
,(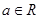 ).
).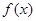 有最值,求实数
有最值,求实数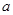 的取值范围;
的取值范围;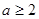 时,若存在
时,若存在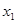 、
、
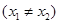 ,使得曲线
,使得曲线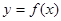 在
在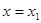 与
与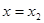 处的切线互相平行,求证:
处的切线互相平行,求证: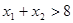 .
.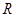 上的函数
上的函数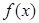 满足:
满足: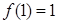 ,且对于任意的
,且对于任意的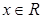 ,都有
,都有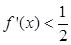 ,则不等式
,则不等式 的解集为 __________________.
的解集为 __________________.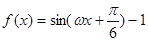
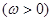 的导数
的导数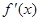 的最大值为3,则
的最大值为3,则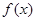 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是 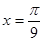
 ,
,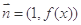 ,
,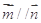 (
(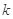 为常数,
为常数, 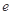 是自然对数的底数),曲线
是自然对数的底数),曲线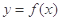 在点
在点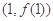 处的切线与
处的切线与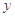 轴垂直,
轴垂直,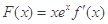 .
.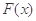 的单调区间;
的单调区间;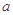 为正实数),若对于任意
为正实数),若对于任意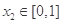 ,总存在
,总存在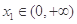 , 使得
, 使得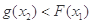 ,求实数
,求实数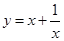 的导数是( )
的导数是( )