题目内容
设函数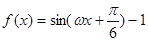
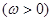 的导数
的导数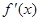 的最大值为3,则
的最大值为3,则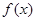 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是
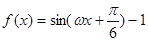
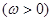 的导数
的导数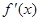 的最大值为3,则
的最大值为3,则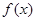 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是 A.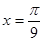 | B.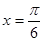 | C.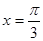 | D.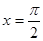 |
A
试题分析:
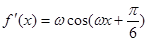 ,最大值为3,ω>0,则ω=3,故
,最大值为3,ω>0,则ω=3,故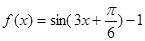 ,
,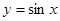 的对称轴在
的对称轴在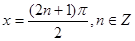 初,则
初,则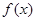 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是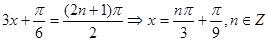 ,选A
,选A
练习册系列答案
相关题目
题目内容
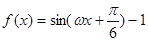
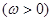 的导数
的导数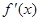 的最大值为3,则
的最大值为3,则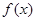 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是 A.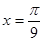 | B.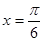 | C.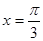 | D.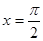 |
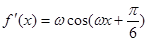 ,最大值为3,ω>0,则ω=3,故
,最大值为3,ω>0,则ω=3,故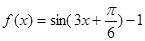 ,
,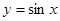 的对称轴在
的对称轴在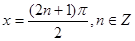 初,则
初,则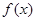 的图象的一条对称轴的方程是
的图象的一条对称轴的方程是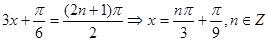 ,选A
,选A