题目内容
已知函数f(x)=x3-3x.
(1)求曲线y=f(x)在点M(2,2)处的切线方程;
(2)求函数f(x)的单调区间;
(3)求函数f(x)的极值(要列出表格).
(1)求曲线y=f(x)在点M(2,2)处的切线方程;
(2)求函数f(x)的单调区间;
(3)求函数f(x)的极值(要列出表格).
(1)∵f'(x)=(x3-3x)'=3x2-3,
∴在点(2,2)处的切线的斜率k=f′(2)=3×22-3=9,
∴切线的方程为y=9x-16.
(2)f(x)=x3-3x,f′(x)=3x2-3,
令f′(x)>0解得x∈(-∞,-1)∪(1,+∞)
令f′(x)<0解得x∈(-1,1),
故函数的单调增区间为(-∞,-1),(1,+∞),单调减区间为(-1,1).
(3)f(x)=x3-3x,
f'(x)=3x2-3=3(x-1)(x+1),
令f'(x)=0,得x=-1或x=1,…(2分)
当x在R上变化时,f'(x)与f(x)的变化情况如下:
故f(x)在R上有极大值为f(-1)=2,极小值为f(1)=-2.
∴在点(2,2)处的切线的斜率k=f′(2)=3×22-3=9,
∴切线的方程为y=9x-16.
(2)f(x)=x3-3x,f′(x)=3x2-3,
令f′(x)>0解得x∈(-∞,-1)∪(1,+∞)
令f′(x)<0解得x∈(-1,1),
故函数的单调增区间为(-∞,-1),(1,+∞),单调减区间为(-1,1).
(3)f(x)=x3-3x,
f'(x)=3x2-3=3(x-1)(x+1),
令f'(x)=0,得x=-1或x=1,…(2分)
当x在R上变化时,f'(x)与f(x)的变化情况如下:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f'(x) | 正 | 0 | 负 | 0 | 正 |
| f(x) | 增 | 极大值 | 减 | 极小值 | 增 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
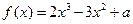 的极大值为
的极大值为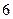 ,则
,则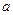 等于( )
等于( )