题目内容
已知f(x)=-
x3+x2+x-1,则过点(2,1)的切线方程是______.
| 1 |
| 2 |
求导函数,可得f′(x)=-
x2+2x+1
若(2,1)为切点,则f′(2)=-1,∴切线方程为y-1=-(x-2),即x+y-3=0
若(2,1)不是切点,设切点坐标为(m,n),则
∴m=0,n=-1,
∴切线方程为y+1=
(x-0),即x-y-1=0,
故答案为:x+y-3=0或x-y-1=0.
| 3 |
| 2 |
若(2,1)为切点,则f′(2)=-1,∴切线方程为y-1=-(x-2),即x+y-3=0
若(2,1)不是切点,设切点坐标为(m,n),则
|
∴m=0,n=-1,
∴切线方程为y+1=
| 1+1 |
| 2-0 |
故答案为:x+y-3=0或x-y-1=0.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
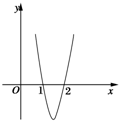
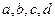 为何值时,函数
为何值时,函数 在
在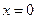 处有极大值
处有极大值 ,在
,在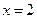 处有极小值
处有极小值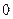 ?
?