题目内容
已知椭圆的两个焦点坐标分别是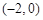 ,
,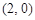 ,并且经过点
,并且经过点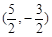 ,求它的标准方程.
,求它的标准方程.
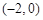 ,
,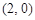 ,并且经过点
,并且经过点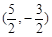 ,求它的标准方程.
,求它的标准方程.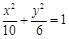 .
.试题分析:解题思路:根据条件设出椭圆的标准方程,再代点求系数即可.规律总结:求圆锥曲线的标准方程通常用待定系数法,即先根据条件设出合适的标准方程,再根据题意得到关于系数的方程或方程组,解之积得.
试题解析:因为椭圆的焦点在x轴上,所以设它的标准方程为
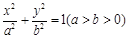 ,
,由椭圆的定义知
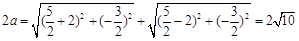 ,
,所以
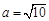 .
.又因为
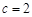 ,
,所以
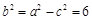 ,
,所以椭圆的标准方程为
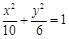 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
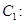
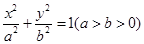 的离心率为
的离心率为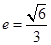 ,过
,过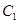 的左焦点
的左焦点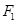 的直线
的直线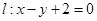 被圆
被圆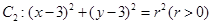 截得的弦长为
截得的弦长为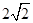 .
.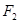 ,在圆
,在圆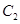 上是否存在点
上是否存在点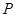 ,满足
,满足 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.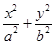 =1(a>0,b>0)的离心率与双曲线
=1(a>0,b>0)的离心率与双曲线 =1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin
=1的一条渐近线的斜率相等以原点为圆心,椭圆的短半轴长为半径的圆与直线sin ·x+cos
·x+cos (O为坐标原点),当
(O为坐标原点),当 时,求实数t取值范围.
时,求实数t取值范围.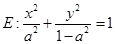 的焦点在
的焦点在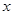 轴上.
轴上.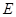 的焦距为1,求椭圆
的焦距为1,求椭圆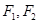 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,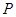 为椭圆
为椭圆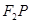 交
交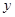 轴与点
轴与点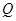 ,并且
,并且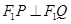 ,证明:当
,证明:当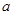 变化时,点
变化时,点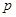 在某定直线上.
在某定直线上. ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是 .
. 满足
满足 ,求椭圆C及其“伴随圆”的方程;
,求椭圆C及其“伴随圆”的方程; 作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为
作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为 ,求P点的坐标;
,求P点的坐标; ,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点
,是否存在a,b,使椭圆C的“伴随圆”上的点到过两点 的直线的最短距离
的直线的最短距离 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
 的离心率为( )
的离心率为( )


