题目内容
已知椭圆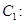
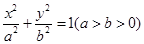 的离心率为
的离心率为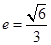 ,过
,过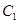 的左焦点
的左焦点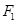 的直线
的直线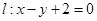 被圆
被圆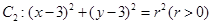 截得的弦长为
截得的弦长为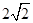 .
.
(1)求椭圆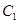 的方程;
的方程;
(2)设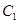 的右焦点为
的右焦点为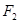 ,在圆
,在圆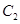 上是否存在点
上是否存在点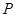 ,满足
,满足 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
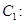
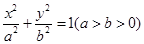 的离心率为
的离心率为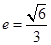 ,过
,过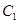 的左焦点
的左焦点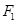 的直线
的直线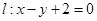 被圆
被圆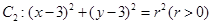 截得的弦长为
截得的弦长为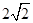 .
.(1)求椭圆
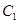 的方程;
的方程;(2)设
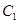 的右焦点为
的右焦点为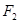 ,在圆
,在圆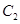 上是否存在点
上是否存在点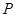 ,满足
,满足 ,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.
,若存在,指出有几个这样的点(不必求出点的坐标);若不存在,说明理由.(1) ;(2)存在.
;(2)存在.
 ;(2)存在.
;(2)存在.试题分析:本题主要考查椭圆的标准方程及其几何性质,点到直线的距离公式、垂径定理、两圆的位置关系等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,利用椭圆的左焦点坐标、离心率联立得到椭圆的基本量a,b,c,从而得到椭圆的标准方程;第二问,先利用点
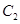 到直线
到直线 的距离公式计算出点到直线的距离,再利用垂径定理求出圆
的距离公式计算出点到直线的距离,再利用垂径定理求出圆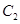 的半径,从而得到圆
的半径,从而得到圆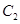 的具体方程,假设圆
的具体方程,假设圆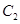 上存在点P满足条件,利用两点间距离公式列出方程,经整理得到一个新的圆,利用2个圆心的距离和半径的关系判断出2个圆相交,所以说明存在两个不同的点P.
上存在点P满足条件,利用两点间距离公式列出方程,经整理得到一个新的圆,利用2个圆心的距离和半径的关系判断出2个圆相交,所以说明存在两个不同的点P.试题解析:因为直线
 的方程为
的方程为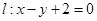 ,
,令
 ,得
,得 ,即
,即 1分
1分∴
 ,又∵
,又∵ ,∴
,∴  ,
, 
∴ 椭圆
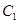 的方程为
的方程为 . 4分
. 4分(2)存在点P,满足

∵ 圆心
 到直线
到直线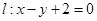 的距离为
的距离为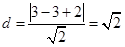 ,
,又直线
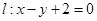 被圆
被圆 截得的弦长为
截得的弦长为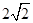 ,
,∴由垂径定理得
 ,
,故圆
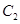 的方程为
的方程为 . 8分
. 8分设圆
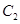 上存在点
上存在点 ,满足
,满足 即
即 ,
,且
 的坐标为
的坐标为 ,
,则
 ,
, 整理得
 ,它表示圆心在
,它表示圆心在 ,半径是
,半径是 的圆。
的圆。∴
 12分
12分故有
 ,即圆
,即圆 与圆
与圆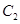 相交,有两个公共点。
相交,有两个公共点。∴圆
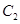 上存在两个不同点
上存在两个不同点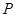 ,满足
,满足 . 14分
. 14分
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 经过椭圆
经过椭圆 的右焦点F及上顶点B,过椭圆外一点(m,0)(
的右焦点F及上顶点B,过椭圆外一点(m,0)( )倾斜角为
)倾斜角为 的直线L交椭圆与C、D两点.
的直线L交椭圆与C、D两点.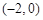 ,
,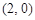 ,并且经过点
,并且经过点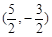 ,求它的标准方程.
,求它的标准方程.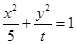 恒有公共点,则t的取值范围是 .
恒有公共点,则t的取值范围是 .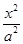 +
+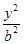 =1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )
=1(a>b>0)上一点P向x轴作垂线,垂足恰为左焦点F1,A是椭圆与x轴正半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP(O是坐标原点),则该椭圆的离心率是( )

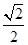

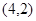 是直线
是直线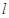 被椭圆
被椭圆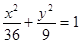 所截得的线段的中点,则直线
所截得的线段的中点,则直线


