Question

椭圆

x2

4

+

y2

3

=1内有一点P（1，-1），F为椭圆的右焦点，在椭圆上有一动点M，则|MP|+|MF|的取值范围为

 

．

Answer 1

分析：设F'为椭圆的左焦点，连结MF'，作过P、F'的直线交椭圆于M₁、M₂两点．根据椭圆的定义算出|MP|+|MF|=|MP|+（2a-|MF'|）=4+（|MP|-|MF'|），由平面几何知识得-|PF'|≤|MP|-|MF'|≤|PF'|，再利用两点间的距离公式加以计算，即可得到|MP|+|MF|的取值范围．

解答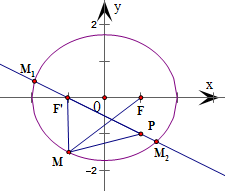：解：设F'为椭圆的左焦点，连结MF'，作过P、F'的直线交椭圆于
M₁、M₂两点，如图所示
∵

x2

4

+

y2

3

=1中，a=2，b=

3

，
∴c=

a2-b2

=1，可得F（1，0），F'（-1，0）．
由椭圆的定义，得|MF|+|MF'|=2a=4，
∴|MP|+|MF|=|MP|+（4-|MF'|）=4+（|MP|-|MF'|）
由平面几何知识，得-|PF'|≤|MP|-|MF'|≤|PF'|，
∴当M与M₁重合时，|MP|-|MF'|达到最大值|PF'|；当M与M₂重合时，|MP|-|MF'|达到最小值-|PF'|．
由|PF'|=

(1+1)2+(-1-0)2

=

5

，可得|MP|-|MF'|的最大值为

5

，最小值为-

5

．
∴|MP|+|MF|=4+（|MP|-|MF'|）的取值范围为[4-

5

，4+

5

]．
故答案为：[4-

5

，4+

5

]．

点评：本题给出椭圆的右焦点为F，点P是椭圆内一个定点，求椭圆上动点M到P、F两点的距离和的范围．着重考查了两点间的距离公式、椭圆的定义与标准方程等知识，属于中档题．