题目内容
【题目】已知数列{an}和{bn}（bn≠0，n∈N*），满足a1=b1=1，anbn+1﹣an+1bn+bn+1bn=0
（1）令cn= 
，证明数列{cn}是等差数列，并求{cn}的通项公式
（2）若bn=2n﹣1 ， 求数列{an}的前n项和Sn ．
【答案】
（1）证明：由anbn+1﹣an+1bn+bn+1bn=0，得
=1，
因为cn= ，
所以cn+1﹣cn=1，
所以数列{cn}是等差数列，所以{cn}=n
（2）由bn=2n﹣1得an=n2n﹣1，
所以Sn=1×20+2×21+3×22+…+n2n﹣1，①
2Sn=1×21+2×22+3×33+…+n2n，②
由②﹣①，得Sn=2n（n﹣1）+1
【解析】（1）数列{an}和{bn}（bn≠0，n∈N*），满足a1=b1=1，anbn+1﹣an+1bn+bn+1bn=0，又cn= ，可得cn+1﹣cn=1，即可证明；（2）利用错位相减法求和即可．
【考点精析】掌握数列的前n项和和数列的通项公式是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
阅读快车系列答案
【题目】某网站对“爱飞客”飞行大会的日关注量x（万人）与日点赞量y（万次）进行了统计对比，得到表格如下：
x | 3 | 5 | 6 | 7 | 9 |
y | 2 | 3 | 3 | 4 | 5 |
由散点图象知，可以用回归直线方程 
来近似刻画它们之间的关系．
（Ⅰ）求出y关于x的回归直线方程，并预测日关注量为10万人时的日点赞量；
（Ⅱ）一个三口之家参加“爱飞客”亲子游戏，游戏规定：三人依次从装有3个白球和2个红球的箱子中不放回地各摸出一个球，大人摸出每个红球得奖金10元，小孩摸出1个红球得奖金50元．求该三口之家所得奖金总额不低于50元的概率．
参考公式：b=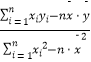 
； 参考数据： 
=200， 
=112．
