题目内容
9.已知椭圆的左焦点为F1,右焦点为F2.若椭圆上存在一点P,满足线段PF2相切于以椭圆的短轴为直径的圆,切点为线段PF2的中点,则该椭圆的离心率为( )| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
分析 设切点为M,连接OM、PF1,通过已知条件可得|PF1|=2b、PF1⊥PF2,进而可得|PF2|=2$\sqrt{{c}^{2}-{b}^{2}}$,利用椭圆的定义便得到2b+2$\sqrt{{c}^{2}-{b}^{2}}$=2a,化简即可得到b=$\frac{2}{3}$,根据离心率的计算公式即可求得离心率e.
解答 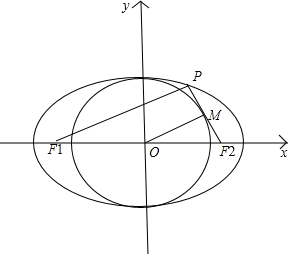 解:如图,设以椭圆的短轴为直径的圆与线段PF2相切于M点,
解:如图,设以椭圆的短轴为直径的圆与线段PF2相切于M点,
连接OM,PF2,
∵M,O分别是PF2,F1F2的中点,
∴MO∥PF1,且|PF1|=2|MO|=2b,
∵OM⊥PF2,∴PF1⊥PF2,|F1F2|=2c,
∴|PF2|=2$\sqrt{{c}^{2}-{b}^{2}}$,
根据椭圆的定义,|PF1|+|PF2|=2a,
∴2b+2$\sqrt{{c}^{2}-{b}^{2}}$=2a,
∴a-b=$\sqrt{{c}^{2}-{b}^{2}}$,
两边平方得:a2-2ab+b2=c2-b2,
∴c2=a2-b2,并代入并化简得:2a=3b,
∴b=$\frac{2}{3}$,a=1,c=$\sqrt{1-\frac{4}{9}}$=$\frac{\sqrt{5}}{3}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{5}}{3}$,
即椭圆的离心率为$\frac{\sqrt{5}}{3}$,
故选:D.
点评 本题考查中位线的性质、圆心和切点的连线和切线的关系,以及椭圆的定义,c2=a2-b2,椭圆离心率的计算公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.若Sn,Tn分别是等差数列{an},{bn}的前n项的和,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{2n+1}{4n-2}$(n∈N*),则$\frac{{a}_{10}}{{b}_{3}+{b}_{18}}$+$\frac{{a}_{11}}{{b}_{6}+{b}_{15}}$=( )
| A. | $\frac{39}{68}$ | B. | $\frac{41}{68}$ | C. | $\frac{39}{78}$ | D. | $\frac{41}{78}$ |
