题目内容
19.已知n条直线l1:x-y+C1=0,l2:x-y+C2=0,l3:x-y+C3=0…,ln:x-y+Cn=0,(其中C1<C2<C3<…<Cn)在这n条平行直线中,每相邻两条直线之间的距离顺次为2,3,4,…,n(即l2直线与直线l1的距离为2,l3直线与直线l2的距离为3,…)(1)若C1=$\sqrt{2}$,求:①C2的值 ②直线x-y+Cn=0与x轴、y轴围成图形的面积S;
(2)若C1=-10$\sqrt{2}$,求直线ln:x-y+Cn=0到原点的距离d,并求dn的最小值.
分析 (1)由平行线的距离公式得$\frac{|{c}_{2}-{c}_{1}|}{\sqrt{2}}$=2,从而解得;②由$\frac{|{c}_{n}-{c}_{1}|}{\sqrt{2}}$=2+3+4+…+n=$\frac{(n+2)(n-1)}{2}$解得cn=$\frac{(n+2)(n-1)}{2}$$\sqrt{2}$+$\sqrt{2}$=$\frac{n(n+1)}{2}$$\sqrt{2}$;从而求面积;
(2)化简cn=$\frac{(n+2)(n-1)}{2}$$\sqrt{2}$-10$\sqrt{2}$,从而求dn=$\frac{|\frac{(n+2)(n-1)}{2}\sqrt{2}-10\sqrt{2}|}{\sqrt{2}}$=|$\frac{{n}^{2}+n-22}{2}$|;从而求最小值.
解答 解:(1)若C1=$\sqrt{2}$,
①由题意,$\frac{|{c}_{2}-{c}_{1}|}{\sqrt{2}}$=2,
即|c2-$\sqrt{2}$|=2$\sqrt{2}$;
又∵C1<C2<C3<…<Cn,
故c2=3$\sqrt{2}$;
②由题意得,$\frac{|{c}_{n}-{c}_{1}|}{\sqrt{2}}$=2+3+4+…+n=$\frac{(n+2)(n-1)}{2}$;
故|cn-$\sqrt{2}$|=$\frac{(n+2)(n-1)}{2}$$\sqrt{2}$;
故cn=$\frac{(n+2)(n-1)}{2}$$\sqrt{2}$+$\sqrt{2}$=$\frac{n(n+1)}{2}$$\sqrt{2}$;
则直线x-y+Cn=0与x轴、y轴围成图形的面积
S=$\frac{1}{2}$•$\frac{n(n+1)}{2}$$\sqrt{2}$•$\frac{n(n+1)}{2}$$\sqrt{2}$=$\frac{{n}^{2}(n+1)^{2}}{4}$;
(2)若C1=-10$\sqrt{2}$,则cn=$\frac{(n+2)(n-1)}{2}$$\sqrt{2}$-10$\sqrt{2}$,
则dn=$\frac{|\frac{(n+2)(n-1)}{2}\sqrt{2}-10\sqrt{2}|}{\sqrt{2}}$=|$\frac{{n}^{2}+n-22}{2}$|;
而d4=1,d5=4;
故dn的最小值为1.
点评 本题考查了数列与函数的综合应用,同时考查了平行线的距离公式与应用,属于中档题.

 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{6}$ | D. | $\frac{{\sqrt{5}}}{3}$ |
| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 286 | 298 | 318 |
(2)利用(1)中所求出的直线方程预测该地2015年的粮食需求量.
(参考公式:$\widehat{b}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)({y}_{1}-y)}{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}-x)^{2}}$=$\frac{\underset{\stackrel{n}{∑}}{n+1}({x}_{1}{y}_{1})-nxy}{\underset{\stackrel{n}{∑}}{n+1}{x}_{1}^{2}-n{x}^{2}}$,$\widehat{a}$=$\widehat{y}-\widehat{b}x$)
| A. | 3x+2y-5=0 | B. | 2x+3y-5=0 | C. | 2x-3y+5=0 | D. | 3x-2y+5=0 |
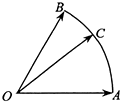 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
| A. | x=-$\frac{π}{2}$ | B. | x=-$\frac{π}{4}$ | C. | x=$\frac{π}{8}$ | D. | x=$\frac{π}{4}$ |
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |