题目内容
【题目】已知函数f(x)= ![]() (a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
(a>0且a≠1)在R上单调递减,且关于x的方程|f(x)|=2﹣x恰好有两个不相等的实数解,则a的取值范围是
【答案】[ ![]() ]∪{
]∪{ ![]() }
}
【解析】解:由y=loga(x+1)+1在[0,+∞) 上递减,得0<a<1,
又由f(x)= ![]() (a>0且a≠1)在R上单调递减,
(a>0且a≠1)在R上单调递减,
得02+3a≥f(0)=1,解得a ![]() ,
,
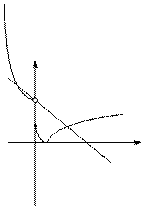
作出函数f(x)= ![]() (a>0且a≠1)在R上的大致图象,
(a>0且a≠1)在R上的大致图象,
由图象可知,在[0,+∞) 上,|f(x)|=2﹣x 有且仅有一个解,
故在(﹣∞,0)上,|f(x)|=2﹣x 同样有且仅有一个解,
当3a>2,即a> ![]() 时,联立|x2+3a|=2﹣x,
时,联立|x2+3a|=2﹣x,
则△=12﹣4(3a﹣2)=0,解得: ![]() ,
,
当1≤3a≤2 时,由图象可知,符合条件.
综上:a∈[ ![]() ]∪{
]∪{ ![]() }.
}.
所以答案是:[ ![]() ]∪{
]∪{ ![]() }.
}.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某技术公司新开发了A,B两种新产品,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种产品各100件进行检测,检测结果统计如下:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
产品A | 8 | 12 | 40 | 32 | 8 |
产品B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计产品A,产品B为正品的概率;
(2)生产一件产品A,若是正品可盈利80元,次品则亏损10元;生产一件产品B,若是正品可盈利100元,次品则亏损20元;在(1)的前提下.记X为生产一件产品A和一件产品B所得的总利润,求随机变量X的分布列和数学期望.
