题目内容
设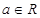 ,函数
,函数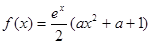 ,其中
,其中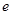 是自然对数的底数。
是自然对数的底数。
(1)判断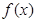 在R上的单调性;
在R上的单调性;
(2)当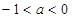 时,求
时,求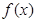 在
在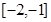 上的最值。
上的最值。
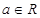 ,函数
,函数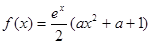 ,其中
,其中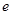 是自然对数的底数。
是自然对数的底数。(1)判断
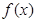 在R上的单调性;
在R上的单调性;(2)当
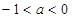 时,求
时,求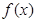 在
在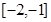 上的最值。
上的最值。(1)当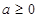 时
时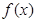 在R上是单调递增函数,当
在R上是单调递增函数,当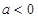 时在
时在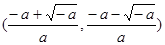 上是单调递增函数,在
上是单调递增函数,在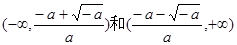 上是单调递减函数(2)
上是单调递减函数(2)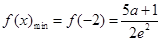 ,
,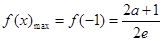
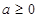 时
时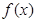 在R上是单调递增函数,当
在R上是单调递增函数,当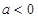 时在
时在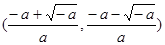 上是单调递增函数,在
上是单调递增函数,在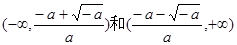 上是单调递减函数(2)
上是单调递减函数(2)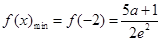 ,
,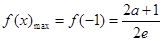
试题分析:(1)对
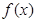 求导,得
求导,得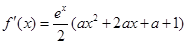 1分
1分设
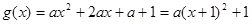
当
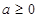 时,
时,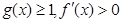
即
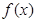 在R上是单调递增函数 3分
在R上是单调递增函数 3分当
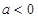 时,
时,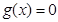 的两根分别为
的两根分别为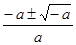
且
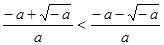
当
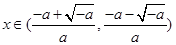 时,
时,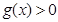
即
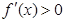
当
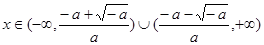 时,
时,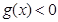
即
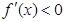
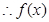 在
在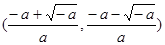 上是单调递增函数;
上是单调递增函数;在
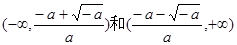 上是单调递减函数 6分
上是单调递减函数 6分(2)当
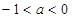 时,
时,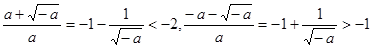
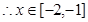 时,
时,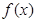 是单调递增函数 10分
是单调递增函数 10分故
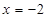 时,
时,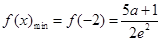
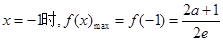 12分
12分点评:当函数解析式中有参数时要对参数分情况讨论确定其单调性,函数在闭区间上的最值出在闭区间的端点或极值点处

练习册系列答案
相关题目
 ,构造函数
,构造函数 的定义如下:当
的定义如下:当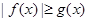 时,
时, ,当
,当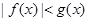 时,
时,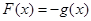 ,则
,则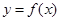 的定义域是
的定义域是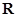 ,若对于任意的正数
,若对于任意的正数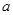 ,函数
,函数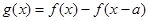 都是其定义域上的减函数,则函数
都是其定义域上的减函数,则函数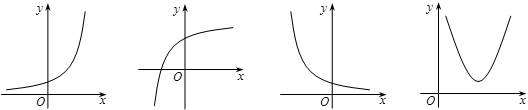
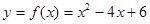 ,
,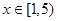 的值域.
的值域.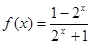 ,请用定义证明
,请用定义证明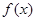 在
在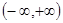
 上为减函数.
上为减函数.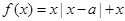 在R上为单调函数,则a的取值范围是 .
在R上为单调函数,则a的取值范围是 .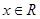 ,奇函数
,奇函数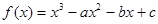 在
在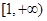 上单调,则实数b的取值范围是__________.
上单调,则实数b的取值范围是__________.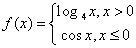 的图象上关于原点
的图象上关于原点 对称的点有 对.
对称的点有 对. 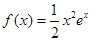 .
.