题目内容
设直2x-3y-1=0与x+y+2=0的交点为P.
(1)直线l经过点P且与直3x+y-1=0垂直,求直线l方程.
(2)求圆心在直线3x+y-1=0上,且经过原点O和点P的圆方程.
(1)直线l经过点P且与直3x+y-1=0垂直,求直线l方程.
(2)求圆心在直线3x+y-1=0上,且经过原点O和点P的圆方程.
由
可得P(-1,-1)
(1)法一:∵直线l与直3x+y-1=0垂直,
∴k=
∴所求直线l方程为y+1=
(x+1)即x-3y-2=0
法二:设过两直线的交点的直线方程为2x-3y-1+λ(x+y+2)=0
即(2+λ)x+(λ-3)y+2λ-1=0
∵l与直3x+y-1=0垂直
∴3(2+λ)+(λ-3)=0
∴∴λ=-
代入可得所求直线的方程为x-3y-2=0
(2)法一:由题意可设圆心为M(a,1-3a)
∵圆经过原点O和点P
∴PM=OM
即
=
解可得a=1
∴圆心(1,-2)半径r=OM=
∴所求圆的方程为(x-1)2+(y+2)2=5
法二:∵圆经过原点O和点P
∴圆心在OP的垂直平分线上,
∵KOP=1,OP的中点(-
,-
)
而OP的垂直平分线为y+
=-(x+
)即x+y+1=0
联立
可得圆心(1,-2),半径r=
∴所求圆的方程为(x-1)2+(y+2)2=5
|
(1)法一:∵直线l与直3x+y-1=0垂直,
∴k=
| 1 |
| 3 |
∴所求直线l方程为y+1=
| 1 |
| 3 |
法二:设过两直线的交点的直线方程为2x-3y-1+λ(x+y+2)=0
即(2+λ)x+(λ-3)y+2λ-1=0
∵l与直3x+y-1=0垂直
∴3(2+λ)+(λ-3)=0
∴∴λ=-
| 3 |
| 4 |
代入可得所求直线的方程为x-3y-2=0
(2)法一:由题意可设圆心为M(a,1-3a)
∵圆经过原点O和点P
∴PM=OM
即
| (a+1)2+(2-3a)2 |
| a2+(1-3a)2 |
解可得a=1
∴圆心(1,-2)半径r=OM=
| 5 |
∴所求圆的方程为(x-1)2+(y+2)2=5
法二:∵圆经过原点O和点P
∴圆心在OP的垂直平分线上,
∵KOP=1,OP的中点(-
| 1 |
| 2 |
| 1 |
| 2 |
而OP的垂直平分线为y+
| 1 |
| 2 |
| 1 |
| 2 |
联立
|
| 5 |
∴所求圆的方程为(x-1)2+(y+2)2=5

练习册系列答案
相关题目
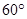 的直线被圆学
的直线被圆学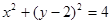 所截得的弦长为(科网 )
所截得的弦长为(科网 )
