题目内容
(本题满分14分)本题共有2个小题,第(1)小题满分6分,第(2)小题满分8分.
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);
(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
某地政府为改善居民的住房条件,集中建设一批经适楼房.用了1400万元购买了一块空地,规划建设8幢楼,要求每幢楼的面积和层数等都一致,已知该经适房每幢楼每层建筑面积均为250平方米,第一层建筑费用是每平方米3000元,从第二层开始,每一层的建筑费用比其下面一层每平方米增加80元.
(1)若该经适楼房每幢楼共
 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数 的表达式(总开发费用=总建筑费用+购地费用);
的表达式(总开发费用=总建筑费用+购地费用);(2)要使该批经适房的每平方米的平均开发费用最低,每幢楼应建多少层?
(1)由已知,每幢经适楼房最下面一层的总建筑费用为:
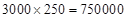 (元)
(元)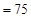 (万元),
(万元),
从第二层开始,每幢每层的建筑总费用比其下面一层多:
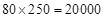 (元)
(元)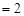 (万元),
(万元),
每幢经适楼房从下到上各层的总建筑费用构成以75为首项,2 为公差的等差数列,2分
所以函数表达式为:
 ; (6分)
; (6分)
(2)由(1)知经适楼房每平方米平均开发费用为:
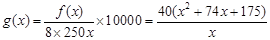 (10分)
(10分)
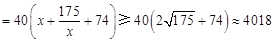 (元) (12分)
(元) (12分)
当且仅当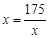 ,即
,即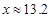 时等号成立,
时等号成立,
但由于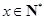 ,验算:当
,验算:当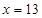 时,
时,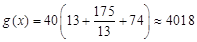 ,当
,当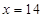 时,
时,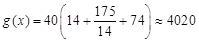 .
.
答:该经适楼建为13层时,每平方米平均开发费用最低. (14分)
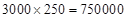 (元)
(元)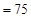 (万元),
(万元),从第二层开始,每幢每层的建筑总费用比其下面一层多:
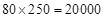 (元)
(元)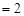 (万元),
(万元),每幢经适楼房从下到上各层的总建筑费用构成以75为首项,2 为公差的等差数列,2分
所以函数表达式为:
 ; (6分)
; (6分)(2)由(1)知经适楼房每平方米平均开发费用为:
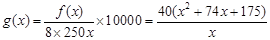 (10分)
(10分)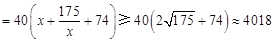 (元) (12分)
(元) (12分)当且仅当
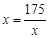 ,即
,即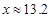 时等号成立,
时等号成立,但由于
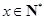 ,验算:当
,验算:当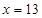 时,
时,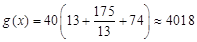 ,当
,当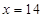 时,
时,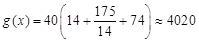 .
.答:该经适楼建为13层时,每平方米平均开发费用最低. (14分)
略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
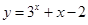 的零点所在的大致区间是(参考数据
的零点所在的大致区间是(参考数据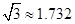 ,
,
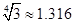 )
)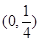
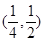
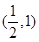
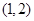
 是定义在
是定义在 上的增函数,且对于任意的
上的增函数,且对于任意的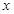 都有
都有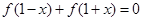 恒成立. 如果实数
恒成立. 如果实数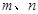 满足不等式组
满足不等式组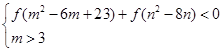 ,那么
,那么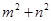 的取值范围是
的取值范围是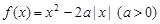 .
.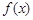 的奇偶性,并写出
的奇偶性,并写出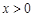 时
时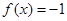 有解,求实数
有解,求实数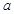 的取值范围.
的取值范围.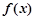 是奇函数,当
是奇函数,当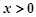 时
时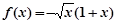 ,当
,当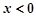 时
时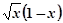
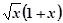
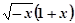
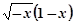
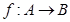 其中
其中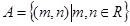 ,
,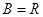 ,已知对所有的有序正整数对
,已知对所有的有序正整数对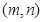 满足下述条件:
满足下述条件: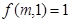 ; 2若
; 2若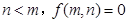
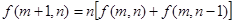
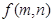 的表达式为 (用含n的代数式表示)
的表达式为 (用含n的代数式表示)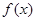 在区间
在区间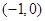 和
和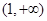 上递增,在区间
上递增,在区间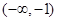 和
和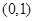 上递减,则
上递减,则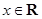 ,函数
,函数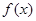 满足
满足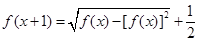 ,设
,设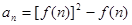 ,数列
,数列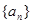 的前15项的和为
的前15项的和为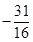 ,则
,则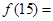 .
.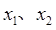 及函数
及函数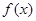 满足
满足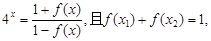 则
则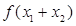 的最小值为_____
的最小值为_____