题目内容
【题目】足球运动被誉为“世界第一运动”.为推广足球运动,某学校成立了足球社团由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如下:
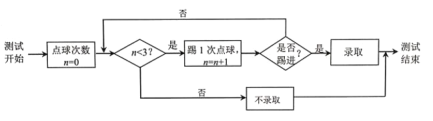
(1)下表是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为![]() ,求
,求![]() ;
;
![]()
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,接到第n次传球的人即为第![]() 次触球者
次触球者![]() ,第n次触球者是甲的概率记为
,第n次触球者是甲的概率记为![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接写出结果即可);
(直接写出结果即可);
(ii)证明:数列![]() 为等比数列.
为等比数列.
【答案】(1)![]() (2)(i)
(2)(i)![]() ,
,![]() ,
,![]() (ii)证明见解析;
(ii)证明见解析;
【解析】
(1)先求出踢一次点球命中的概率,然后根据相互独立事件的乘法公式分别求出![]() 取1,2,3的概率,再根据离散型随机变量的期望公式可求得结果;
取1,2,3的概率,再根据离散型随机变量的期望公式可求得结果;
(2)(i)根据传球顺序分析可得答案;(ii)根据题意可得![]() ,再变形为
,再变形为![]() ,根据等比数列的定义可证结论.
,根据等比数列的定义可证结论.
(1)这150个点球中的进球频率为![]() ,
,
则该同学踢一次点球命中的概率![]() ,
,
由题意,![]() 可能取1,2,3,则
可能取1,2,3,则
![]() ,
,![]() ,
,![]() ,
,
则![]() 的期望
的期望![]() .
.
(2)(i)因为从甲开始随机地将球传给其他两人中的任意一人,所以第1次触球者是甲的概率![]() ,显然第2次触球者是甲的概率
,显然第2次触球者是甲的概率![]() ,第2次传球有两种可能,所以第3次触球者是甲的概率概
,第2次传球有两种可能,所以第3次触球者是甲的概率概![]() ,
,
(ii)∵第n次触球者是甲的概率为![]() ,
,
所以当![]() 时,第
时,第![]() 次触球者是甲的概率为
次触球者是甲的概率为![]() ,第
,第![]() 次触球者不是甲的概率为
次触球者不是甲的概率为![]() ,
,
则![]() .
.
从而![]() ,又
,又![]() ,
,
∴![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.
的等比数列.

【题目】闰月年指农历里有闰月的年份,比如2020年是闰月年,4月23日至5月22日为农历四月,5月23日至6月20日为农历闰四月.农历置闰月是为了农历年的平均长度接近回归年:农历年中的朔望月的平均长度为29.5306日,![]() 日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
日,回归年的总长度为365.2422日,两者相差10.875日.因此,每19年相差206.625日,约等于7个朔望月.这样每19年就有7个闰月年.以下是1640年至1694年间所有的闰月年:
1640 | 1642 | 1645 | 1648 | 1651 | 1653 | 1656 |
1659 | 1661 | 1664 | 1667 | 1670 | 1672 | 1675 |
1678 | 1680 | 1 683 | 1686 | 1689 | 1691 | 1694 |
则从2020年至2049年,这30年间闰月年的个数为( )
A.10B.11C.12D.13