题目内容
【题目】设两向量e1、e2满足| 
|=2，| 
|=1， 、 的夹角为60°，若向量2t +7 与向量 +t 的夹角为钝角，求实数t的取值范围．
【答案】解： 
2=4， 
2=1， =2×1×cos60°=1， ∴（2t +7 ）（ +t ）=2t 2+（2t2+7） +7t 2=2t2+15t+7．
∴2t2+15t+7＜0．
∴﹣7＜t＜﹣ 
．设2t +7 =λ（ +t ）（λ＜0） 
2t2=7t=﹣ 
，
∴λ=﹣ 
．
∴当t=﹣ 时，2t +7 与 +t 的夹角为π．
∴t的取值范围是（﹣7，﹣ ）∪（﹣ ，﹣ ）
【解析】欲求实数t的取值范围，先根据条件，利用向量积的运算求出（2t 
+7 
）（ +t ）的值，由于夹角为钝角，所以计算得到的值是负值，最后解出这个不等式即可得到实数t的取值范围．
【考点精析】本题主要考查了数量积表示两个向量的夹角的相关知识点，需要掌握设
、
都是非零向量，
，
，
是与
的夹角，则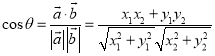
才能正确解答此题．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
