Question

【题目】解关于x的不等式（m+1）x2﹣4x+1≤0（m∈R）

Answer 1

【答案】解：∵（m+1）x2﹣4x+1≤0（m∈R）， （i）当m=﹣1时，原不等式为﹣4x+1≤0，解集为{x|x }，
（ii）当m＜﹣1时，
解方程（m+1）x2﹣4x+1=0，得x= = ，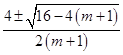
原不等式的解集为{x|x≥ 或 }．
（iii）当﹣1＜m＜3时，
解方程（m+1）x2﹣4x+1=0，
得x= = ，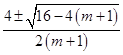
原不等式的解集为{x| ≤x≤ }，
（iv）当m=3时，原不等式为4x2﹣4x+1≤0，解集为{x|x= }，
（v）当m＞3时，方程（m+1）x2﹣4x+1=0无解，
原不等式的解集．
【解析】由m=﹣1，m＜﹣1，﹣1＜m＜3，m=3，m＞3，进行分类讨论，由此能求出关于x的不等式（m+1）x2﹣4x+1≤0（m∈R）的解集．
【考点精析】本题主要考查了解一元二次不等式的相关知识点，需要掌握求一元二次不等式解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边才能正确解答此题．