题目内容
6.设公差不为零,各项均为正数的等差数列{an}满足a2=$\sqrt{{8a}_{1}+1}$,且a1,a3,a13构成等比数列.(1)求数列{an}的通项公式;
(2)若bn=$\frac{1}{\sqrt{{a}_{n}}}$,数列{bn}的前n项和为Sn,求证:Sn>$\sqrt{2n+1}$-1.
分析 (1)利用$({a}_{1}+2d)^{2}$=a1(a1+12d)、$\sqrt{{8a}_{1}+1}$=a1+d化简可知数列{an}是以1为首项、2为公差的等差数列,进而计算可得结论;
(2)通过an=2n-1可知bn=$\frac{1}{\sqrt{2n-1}}$,利用数学归纳法证明即可.
解答 (1)解:由题可知:$({a}_{1}+2d)^{2}$=a1(a1+12d),
化简得:4d2=8a1d,
又∵公差d不为零,
∴d=2a1,
∴$\sqrt{{8a}_{1}+1}$=a2=a1+d=3a1,
解得:a1=1或a1=-$\frac{1}{9}$(舍),
∴数列{an}是以1为首项、2为公差的等差数列,
故其通项公式an=1+2(n-1)=2n-1;
(2)证明:∵an=2n-1,
∴bn=$\frac{1}{\sqrt{{a}_{n}}}$=$\frac{1}{\sqrt{2n-1}}$,
下面用数学归纳法来证明:Sn>$\sqrt{2n+1}$-1.
①当n=1时,命题显然成立;
②假设当n=k(>1)时命题也成立,即Sk>$\sqrt{2k+1}$-1,
∴Sk+bk+1>$\sqrt{2k+1}$-1+bk+1,
即Sk+1>$\sqrt{2k+1}$-1+$\frac{1}{\sqrt{2k+1}}$,
∵(2k+2)2>(2k+1)(2k+3),
∴2k+1+1>$\sqrt{(2k+1)}$•$\sqrt{2k+3}$,
∴$\sqrt{2k+1}$+$\frac{1}{\sqrt{2k+1}}$>$\sqrt{2k+3}$,
即Sk+1>$\sqrt{2k+3}$-1,
∴当n=k+1时,命题也成立;
由①、②可知:Sn>$\sqrt{2n+1}$-1.
点评 本题考查数列的通项及n项和,考查运算求解能力,注意解题方法的积累,属于中档题.

 备战中考寒假系列答案
备战中考寒假系列答案| A. | p1+p2 | B. | p1•p2 | C. | 1-p1•p2 | D. | 1-(1-p1)•(1-p2) |
| 赔付金额(元) | 0 | 1000 | 2000 | 3000 | 4000 |
| 车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获陪金额为4000元的概率.
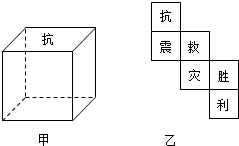 如图甲,水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图乙是一个正方体的表面展开图,若图中“抗”在正方体的上面,则这个正方体的下面是( )
如图甲,水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图乙是一个正方体的表面展开图,若图中“抗”在正方体的上面,则这个正方体的下面是( )