下列函数中.与函数的奇偶性.单调性均相同的是A．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

下列函数中，与函数的奇偶性、单调性均相同的是( )

A．

B．

C．

D．

解析试题分析：因为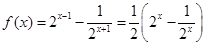函数，可知函数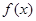在定义域上是奇函数，且单调递增，为非奇非偶函数，为偶函数，在定义域上是奇函数，但不单调递增，只有在定义域上是奇函数，且单调递增，故选Ｂ．
考点：函数的性质．

练习册系列答案

高中学业水平考试复习学与练指导精编丛书系列答案

高效复习计划小学毕业升学总复习系列答案

优加学案口算题卡系列答案

全真模拟试卷精编系列答案

相关题目

对于函数，若存在区间，使得，则称函数为“可等域函数”，区间为函数的一个“可等域区间”．给出下列4个函数：
①；②； ③； ④．
其中存在唯一“可等域区间”的“可等域函数”为（）

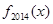函数则函数是（）

A．奇函数但不是偶函数	B．偶函数但不是奇函数
C．既是奇函数又是偶函数	D．既不是奇函数又不是偶函数

已知函数，若函数在上有两个零点，则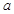的取值范围是

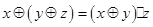对非零实数,定义运算满足:(1); (2).若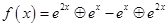,则下列判断正确的是( )

A．是增函数又是奇函数	B．是减函数又是奇函数
C．是增函数又是偶函数	D．是减函数又是偶函数

下列函数中既是偶函数，又是区间(－1，0)上的减函数的是( )

已知函数是定义在R上的偶函数, 且在区间单调递增．若实数满足,则的取值范围是（）

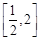下列各组函数表示同一函数的是（）

A．	B．
C．	D．

已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增.若实数a满足f(log₂a)+f(a)≤2f(1),则a的取值范围是(　　)

试题分类