题目内容
5.已知a+b=$\sqrt{2}sin(θ+\frac{π}{4}),a-b=\sqrt{2}sin(θ-\frac{π}{4}),求证:{a^2}+{b^2}$=1.分析 首先,根据已知条件,得到a=sinθ,b=cosθ,然后,根据同角三角函数基本关系式进行处理即可.
解答 证明:∵a+b=$\sqrt{2}$sin(θ+$\frac{π}{4}$)=sinθ+cosθ
a-b=$\sqrt{2}$sin($θ-\frac{π}{4}$)=sinθ-cosθ,
∴a=sinθ,b=cosθ,
∴a2+b2=1,
∴原等式成立.
点评 本题重点考查了三角恒等变换公式、同角三角函数基本关系式、三角函数的基本性质等知识,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.将一个表面积为24的正方体切成27个全等的小正方体,则表面积增加( )
| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
13.已知一组数据为-8,-1,4,x,10,13且这组数的中位数是7,那么数据中的众数是( )
| A. | 7 | B. | 6 | C. | 4 | D. | 10 |
20.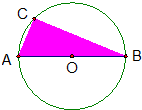 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
 如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )
如图,点C为半径是1的圆上一点,且劣弧长AC是劣弧长CB的一半,假设你在这个图形上随机地撒一粒豆子,则∠ABC及豆子落在阴影区域的概率分别是( )| A. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2π}$ | B. | $\frac{π}{3}$,$\frac{\sqrt{3}}{2π}$ | C. | $\frac{π}{6}$,$\frac{\sqrt{3}}{2}$ | D. | $\frac{π}{6}$,$\frac{3}{2π}$ |
14.已知椭圆E的中心在原点,一个焦点为F(1,0),定点A(-1,1)在E的内部,若椭圆E上存在一点P使得|PA|+|PF|=7,则椭圆E的方程可以是( )
| A. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{2}$=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | C. | $\frac{{x}^{2}}{8}$+$\frac{{y}^{2}}{7}$=1 | D. | $\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{8}$=1 |
15.已知|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{5}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |