题目内容
设函数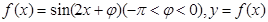 图象的一条对称轴是直线
图象的一条对称轴是直线 .
.
(1)求 ;
;
(2)求f(x)的最小正周期、单调增区间及对称中心.
(1)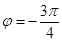 ;(2)
;(2)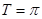 ;
;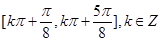 ;
; .
.
解析试题分析:(1)由三角函数的图象和性质可知:函数 的对称轴均是通过函数图象的最高点或最低点向x轴所引的垂线,既然函数
的对称轴均是通过函数图象的最高点或最低点向x轴所引的垂线,既然函数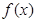 图象的一条对称轴是直线
图象的一条对称轴是直线 ,所以函数
,所以函数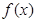 在
在 处取得最值,从而
处取得最值,从而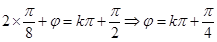 ,又因为
,又因为 ,从而可求得
,从而可求得 的值;(2)由三角函数的图象和性质可知:函数
的值;(2)由三角函数的图象和性质可知:函数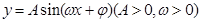 的最小正周期为
的最小正周期为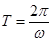 ,单调增区间由不等式:
,单调增区间由不等式: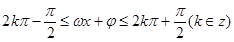 求得,对称中心的横坐标由
求得,对称中心的横坐标由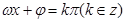 求得,而纵标为零;将(1)结果及已知代入上边公式即可求得对应结果.
求得,而纵标为零;将(1)结果及已知代入上边公式即可求得对应结果.
试题解析:(1)由条件知: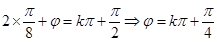

∵ ,∴
,∴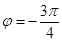
(2)f(x)的最小正周期为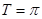 ,由
,由
得递增区间为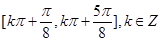 ;对称中心为
;对称中心为
考点:三角函数的图象和性质.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 .
. 的值;
的值; 的值.
的值. ,函数
,函数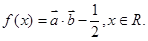
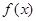 的最小值和最小正周期;
的最小值和最小正周期;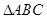 的内角
的内角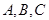 的对边分别为
的对边分别为 ,且
,且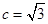 ,
,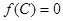 ,若
,若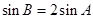 ,求
,求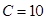 ,面积
,面积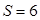 ,求这个扇形的半径
,求这个扇形的半径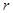 和圆心角
和圆心角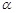 的弧度数.
的弧度数.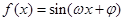 (
(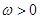 ,
,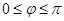 )为偶函数,其图象上相邻的两个对称轴之间的距离为
)为偶函数,其图象上相邻的两个对称轴之间的距离为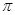 .
.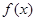 的解析式;
的解析式;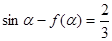 ,求
,求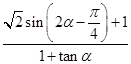 的值.
的值.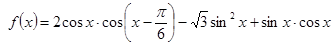
 的最小正周期;
的最小正周期; 时,若
时,若 ,求
,求 的值.
的值.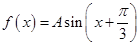 ,
, ,且
,且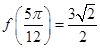 .
.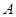 的值;
的值;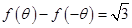 ,
,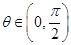 ,求
,求 .
.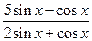 =______.
=______.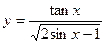 的定义域为 .
的定义域为 .