题目内容
已知 ,函数
,函数
(1)求函数 的最小值和最小正周期;
的最小值和最小正周期;
(2)设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,
, ,若
,若 ,求
,求 的面积.
的面积.
(1) 的最小值为
的最小值为 ,最小正周期为
,最小正周期为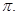 (2)
(2)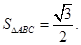
解析试题分析:(1)利用两角和正弦公式和降幂公式化简,得到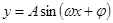 的形式,利用公式
的形式,利用公式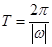 计算周期.(2)求三角函数的最小正周期一般化成
计算周期.(2)求三角函数的最小正周期一般化成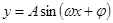 ,
,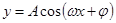 ,
,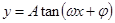 形式,利用周期公式即可.(3)求解较复杂三角函数的最值时,首先化成
形式,利用周期公式即可.(3)求解较复杂三角函数的最值时,首先化成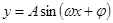 形式,在求最大值或最小值;(4)1)在解决三角形的问题中,面积公式
形式,在求最大值或最小值;(4)1)在解决三角形的问题中,面积公式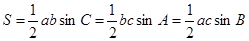 最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.
最常用,因为公式中既有边又有角,容易和正弦定理、余弦定理联系起来.
试题解析:解:(1)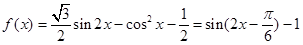 ,
, 的最小值为
的最小值为 ,最小正周期为
,最小正周期为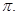 3分
3分
(2)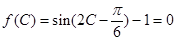 ,则
,则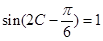 .
.
∵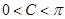 ,∴
,∴ ,因此
,因此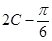 =
= ,∴
,∴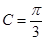 . 5分
. 5分
∵ 及正弦定理,得
及正弦定理,得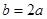 .①
.①
由余弦定理,得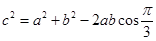 ,且
,且 ,
,
∴ . ②
. ②
由①②联立,得 ,
,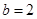 . 7分
. 7分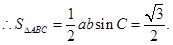 8分
8分
考点:(1)三角函数的化简和求值;(2)求三角形的面积.

练习册系列答案
相关题目
 ,
, , 且
, 且 .
. 的解析式;
的解析式; 时,
时,  的值.
的值.
 图象的一条对称轴是直线
图象的一条对称轴是直线 .
.  ;
; ,再将图像沿
,再将图像沿 轴向右平移
轴向右平移 个单位,得到函数
个单位,得到函数 的图像.
的图像. .
. 上的值域.
上的值域.
 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;  ,且
,且 时,求
时,求 的值.
的值. 的最小正周期为
的最小正周期为
 的值;
的值; 的图像是由
的图像是由 的图像向右平移
的图像向右平移 个单位长度得到,求
个单位长度得到,求 =________.
=________.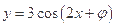 的图象关于点
的图象关于点 中心对称,则
中心对称,则 的最小值为 .
的最小值为 .