题目内容
椭圆 的右焦点为F,其右准线与
的右焦点为F,其右准线与 轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是( )
轴的交点为A,在椭圆上存在点P满足线段AP的垂直平分线过点F,则椭圆离心率的取值范围是( )
A.(0,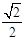 ] ] | B.(0, ] ] | C.[ ,1) ,1) | D.[ ,1) ,1) |
D
解析试题分析:本题关键是建立一个不等关系,线段AP的垂直平分线过点F,说明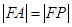 ,
,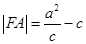
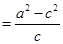 ,因此已知条件转化为以
,因此已知条件转化为以 为圆心,以
为圆心,以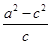 为半径的圆与椭圆相交,从而得
为半径的圆与椭圆相交,从而得 ,
,
则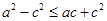 ,∴
,∴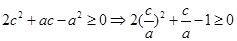 ,即
,即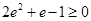 ,所以
,所以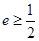 ,因此
,因此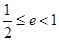 .
.
考点:椭圆的离心率.

练习册系列答案
相关题目
已知直线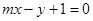 交抛物线
交抛物线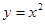 于
于 、
、 两点,则△
两点,则△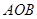 ( )
( )
| A.为直角三角形 | B.为锐角三角形 |
| C.为钝角三角形 | D.前三种形状都有可能 |
设 、
、 是曲线
是曲线 上的点,
上的点, ,则必有 ( )
,则必有 ( )
A. | B.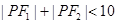 |
C. | D. |
椭圆 的焦距为( )
的焦距为( )
| A.10 | B.5 | C. | D. |
设椭圆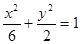 和双曲线
和双曲线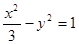 的公共焦点为
的公共焦点为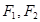 ,
,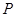 是两曲线的一个公共点,则cos
是两曲线的一个公共点,则cos 的值等于( )
的值等于( )
A.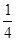 | B.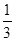 | C. | D.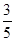 |
已知双曲线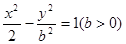 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为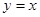 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· = ( )
= ( )
| A.-12 | B.-2 | C. 0 | D.4 |
方程 表示的曲线是( )
表示的曲线是( )
A.焦点在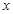 轴上的椭圆 轴上的椭圆 | B.焦点在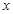 轴上的双曲线 轴上的双曲线 |
C.焦点在 轴上的椭圆 轴上的椭圆 | D.焦点在 轴上的双曲线 轴上的双曲线 |
已知 <4,则曲线
<4,则曲线 和
和 有( )
有( )
| A.相同的准线 | B.相同的焦点 | C.相同的离心率 | D.相同的长轴 |


