题目内容
7.已知f(x)=alnx,g(x)=-x2+3x-2.(1)当a=1时,求f(x),g(x)在x=1处的切线;
(2)讨论函数h(x)=f(x)-g(x)的单调性;
(3)若f(x)>g(x)在x>1时恒成立,求a的取值范围.
分析 (1)当a=1时,分别求出两个切点坐标,和导函数的函数值,代入直线的点斜式方程,可得答案.;
(2)h(x)=f(x)-g(x)=alnx+x2-3x+2.求导后,分别讨论定义域内各个区间上导函数的符号,进而可得函数h(x)=f(x)-g(x)的单调性;
(3)结合(2)中结论,可得若f(x)>g(x)在x>1时恒成立,则h(x)>0在x>1时恒成立,进而得到满足条件的a的取值范围.
解答 解:(1)∵当a=1时,f(x)=lnx,g(x)=-x2+3x-2.
∴f′(x)=$\frac{1}{x}$,g(x)=-2x2+3.
∴f′(1)=1,g(1)=1,
又∵f(1)=0,g(1)=0.
故f(x),g(x)在x=1处的切点坐标均为(1,0)点,切线斜率均为1,
故f(x),g(x)在x=1处的切线方程为:y=x-1,即x-y-1=0,
(2)∵h(x)=f(x)-g(x)=alnx+x2-3x+2.
∴h′(x)=$\frac{a}{x}$+2x-3=$\frac{2{x}^{2}-3x+a}{x}$
当a$≥\frac{9}{8}$时,h′(x)≥0在(0,+∞)上恒成立,此时函数h(x)在(0,+∞)上单调递增;
当0<a<$\frac{9}{8}$时,令h′(x)=0,则x=$\frac{3-\sqrt{9-8a}}{4}$,或x=$\frac{3+\sqrt{9-8a}}{4}$,
此时x∈(0,$\frac{3-\sqrt{9-8a}}{4}$),或x∈($\frac{3+\sqrt{9-8a}}{4}$,+∞)时,h′(x)>0函数h(x)为增函数,
x∈($\frac{3-\sqrt{9-8a}}{4}$,$\frac{3+\sqrt{9-8a}}{4}$)时,h′(x)<0函数h(x)为减函数,
当a≤0时,令h′(x)=0,则x=$\frac{3+\sqrt{9-8a}}{4}$,
此时x∈($\frac{3+\sqrt{9-8a}}{4}$,+∞)时,h′(x)>0函数h(x)为增函数,
x∈(0,$\frac{3+\sqrt{9-8a}}{4}$)时,h′(x)<0函数h(x)为减函数,
(3)若f(x)>g(x)在x>1时恒成立,
则h(x)>0在x>1时恒成立,
由(2)得:
当a$≥\frac{9}{8}$时,h(1)=0,满足h(x)>0在x>1时恒成立,
当0<a<$\frac{9}{8}$时,若h(x)>0在x>1时恒成立,则$\frac{3+\sqrt{9-8a}}{4}$≤1,
解得:1≤a<$\frac{9}{8}$,
当a≤0时,$\frac{3+\sqrt{9-8a}}{4}$>1,此时h($\frac{3+\sqrt{9-8a}}{4}$)<1,不满足条件;
综上所述,若f(x)>g(x)在x>1时恒成立,a≥1
点评 本题考查的知识点是利用导数研究函数的单调性,利用导数研究函数的最值,恒成立问题,导数法研究函数的切线,难度中档.

| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{1}{4}$ | C. | -$\frac{\sqrt{6}}{2}$ | D. | ±$\frac{\sqrt{6}}{2}$ |
| A. | (-2,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,+∞] | C. | (-∞,-2) | D. | (0,$\frac{1}{2}$) |
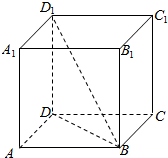 在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.
在正方体ABCD-A1B1C1D1中,对角线BD1分别与平面AC,平面BC1,平面BA1所成的角,并求这些角的余弦值.