题目内容

18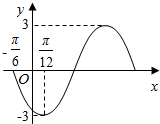．函数y=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜π）的部分图象如图所示，则其解析式是y=3sin（2x-$\frac{2π}{3}$）．

分析 由题意求出函数的周期，最大值A，利用函数经过的特殊点，求出ϕ，即可求出函数的解析式．

解答 解：由题意以及函数的图象可知，A=3，T=4×（$\frac{π}{12}+\frac{π}{6}$）=π，
所以ω=2，因为函数的图象经过（$\frac{π}{12}$，-3），
所以-3=3sin（2×$\frac{π}{12}$+ϕ），|ϕ|＜π，所以ϕ=-$\frac{2π}{3}$，
所以函数的解析式为：y=3sin（2x-$\frac{2π}{3}$）．
故答案为：y=3sin（2x-$\frac{2π}{3}$）．

点评 本题考查函数的解析式的求法，注意函数的图象的特征是解题的关键，考查计算能力．

练习册系列答案
相关题目
8．已知向量$\overrightarrow a$、$\overrightarrow b$满足$|\overrightarrow a|=1$，$\overrightarrow b=（-2，3）$，且$λ\overrightarrow a+\overrightarrow b=\overrightarrow 0$（λ∈R），则|λ|=$\sqrt{13}$．
9．已知函数f（x）=$\frac{1+{x}^{2}}{1-{x}^{2}}$，求：
（1）求它的定义域；
（2）f（a）+f（$\frac{1}{a}$）的值．
（3）f（$\frac{1}{2}$）+f（$\frac{1}{3}$）+f（-2）+f（-3）的值．
6．命题P：?x∈R，$x+\frac{1}{x}＜a$成立，则P的否定为（　　）
A．?x∈R，$x+\frac{1}{x}＞a$成立B．?x∈R，$x+\frac{1}{x}＜a$成立C．?x∈R，$x+\frac{1}{x}≥a$成立D．?x∈R，$x+\frac{1}{x}≤a$成立
13．已知函数y=f（x），对于任意的x$∈[0，\frac{π}{2}）$满足f′（x）cosx+f（x）sinx＞0，则下列不等式中成立的有②③④．
①$\sqrt{2}f（\frac{π}{3}）$＜f（$\frac{π}{4}$） ②$\sqrt{2}$f（$\frac{π}{6}$）$＜\sqrt{3}$f（$\frac{π}{4}$） ③f（0）$＜\sqrt{2}$f（$\frac{π}{4}$） ④f（$\frac{π}{6}$）$＜\sqrt{3}$f（$\frac{π}{3}$）
3．已知直线l过定点P（1，0）且与圆C：（x-2）2+（y-2）2=4相交于A、B两点
（1）若直线l的倾斜角为$\frac{π}{4}$，求线段AB中点为M的坐标
（2）求当△ABC的面积最大时直线l的方程．
10．若非零函数f（x）对任意实数a，b均有f（a+b）=f（a）•f（b），且当x＜0时，f（x）＞1．
（1）求f（0）的值；
（2）求证：f（x）＞0对一切实数x∈R都成立；
（3）当f（4）=$\frac{1}{16}$时，解不等式f（x-3）•f（5-x2）≤$\frac{1}{4}$．
7．已知f（x）=mx2+nx-2（n＞0，m＞0）的图象与x轴交与（2，0），则$\frac{1}{m}+\frac{2}{n}$的最小值为8．
8．一个球的体积等于其表面积，那么这个球的半径为（　　）
A．$\frac{1}{2}$B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网