题目内容
【题目】如图,在四棱锥P-ABCD中,平面PAD ![]() 平面ABCD,PA
平面ABCD,PA ![]() PD ,PA=PD,AB
PD ,PA=PD,AB ![]() AD,AB=1,AD=2,AC=CD=
AD,AB=1,AD=2,AC=CD= ![]() ,
, 
(1)求证:PD ![]() 平面PAB;
平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;
(3)在棱PA上是否存在点M,使得BMll平面PCD?若存在,求 ![]() 的值;若不存在,说明理由。
的值;若不存在,说明理由。
【答案】
(1)
证明:∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
且AB⊥AD,AB平面ABCD,
∴AB⊥平面PAD,
∵PD平面PAD,
∴AB⊥PD,
又PD⊥PA,且PA∩AB=A,
∴PD⊥平面PAB;
(2)
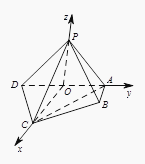
解:如图:
取 ![]() 中点为
中点为 ![]() ,连结
,连结 ![]() ,
, ![]()
∵ ![]()
∴ ![]()
![]()
![]()
∵ ![]()
∴ ![]()
![]()
![]()
以 ![]() 为原点,如图建系
为原点,如图建系
易知P(0,0,1),B(1,1,0),D(0,﹣1,0),C(2,0,0),
则 ![]() ,
, ![]() ,
, ![]() ,
, ![]()
设 ![]() 为面
为面 ![]() 的法向量,令
的法向量,令 ![]()
 ,则
,则 ![]() 与面
与面 ![]() 夹角
夹角 ![]() 有
有

(3)
解:假设存在 ![]() 点使得
点使得 ![]() 面
面 ![]()
设 ![]() ,
, ![]()
由(2)知 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
有 ![]()
∴ ![]()
∵ ![]() 面
面 ![]() ,
, ![]() 为
为 ![]() 的法向量
的法向量
∴ ![]()
即 ![]()
∴ ![]()
∴综上,存在 ![]() 点,即当
点,即当 ![]() 时,
时, ![]() 点即为所求
点即为所求
【解析】(1)由已知结合面面垂直的性质可得AB⊥平面PAD,进一步得到AB⊥PD,再由PD⊥PA,由线面垂直的判定得到PD⊥平面PAB;
(2)取AD中点为O,连接CO,PO,由已知可得CO⊥AD,PO⊥AD.以O为坐标原点,建立空间直角坐标系,求得P(0,0,1),B(1,1,0),D(0,﹣1,0),C(2,0,0),进一步求出向量 ![]() 的坐标,再求出平面PCD的法向量
的坐标,再求出平面PCD的法向量 ![]() ,设PB与平面PCD的夹角为θ,由
,设PB与平面PCD的夹角为θ,由 ![]() 求得直线PB与平面PCD所成角的正弦值;
求得直线PB与平面PCD所成角的正弦值;
(3)假设存在M点使得BM∥平面PCD,设 ![]() ,M(0,y1 , z1),由
,M(0,y1 , z1),由 ![]() 可得M(0,1﹣λ,λ),
可得M(0,1﹣λ,λ), ![]() ,由BM∥平面PCD,可得
,由BM∥平面PCD,可得 ![]() ,由此列式求得当
,由此列式求得当 ![]() 时,M点即为所求.
时,M点即为所求.
【考点精析】根据题目的已知条件,利用空间中直线与平面之间的位置关系的相关知识可以得到问题的答案,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
