题目内容
已知 =(1,2),
=(1,2), =(-2,n) (n>1),
=(-2,n) (n>1), 与
与 的夹角是45°.
的夹角是45°.
(1)求 ;
;
(2)若 与
与 同向,且
同向,且 与
与 -
- 垂直,求
垂直,求 .
.
(1) =(-2,6);(2)
=(-2,6);(2) =(-1,3);
=(-1,3);
解析试题分析:(1)由向量数量积的坐标表示得 ·
· =2n-2,又由数量积公式可得cos 45°=
=2n-2,又由数量积公式可得cos 45°=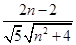 =
=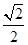 ,所以可以求得
,所以可以求得 ;(2)由
;(2)由 与
与 -
- 垂直得,(
垂直得,( -
- )·
)· =0,又结合
=0,又结合 与
与 同向,可设
同向,可设 =λ
=λ (λ>0),带入计算可得λ的值,λ算出后,即可得
(λ>0),带入计算可得λ的值,λ算出后,即可得 。
。
试题解析:解:(1) ·
· =2n-2,|
=2n-2,| |=
|=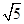 ,|
,| |=
|=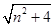 ,
,
∴cos 45°=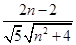 =
=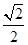 ,∴3n2-16n-12=0,∴n=6或n=-
,∴3n2-16n-12=0,∴n=6或n=- (舍),∴
(舍),∴ =(-2,6).
=(-2,6).
(2)由(1)知, ·
· =10,|
=10,| |2=5.又
|2=5.又 与
与 同向,故可设
同向,故可设 =λ
=λ (λ>0),(
(λ>0),( -
- )·
)· =0,
=0,
∴λ ·
· -|
-| |2=0,∴λ=
|2=0,∴λ=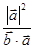 =
=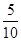 =
=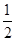 ,∴
,∴ =
=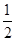
 =(-1,3).
=(-1,3).
考点:1、向量的坐标运算及数量积;2、向量垂直的坐标运算;

练习册系列答案
相关题目
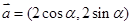 ,
,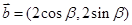 ,且直线
,且直线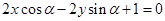 与圆
与圆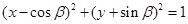 相切,则向量
相切,则向量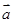 与
与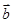 的夹角为______.
的夹角为______. ,
, ,当
,当 为何值时,
为何值时,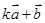 与
与 垂直?(2)
垂直?(2) 与
与 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?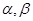 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点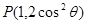 在角
在角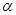 的终边上,点Q
的终边上,点Q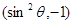 在角
在角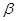 的终边上,且
的终边上,且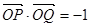 .
.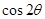 ;
; 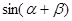 的值.
的值. ,
, ,且
,且 .
. 及
及 ;
; 的最小值为
的最小值为 ,求实数
,求实数 的值.
的值. 中,
中, ,
, ,设
,设 .
. 时,求
时,求 的值;
的值; ,求
,求 的值.
的值. ,
, ,且
,且 .
. 的轨迹
的轨迹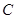 的方程;
的方程; 相交于不同的两点
相交于不同的两点 ,又点
,又点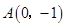 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围. 为坐标原点,
为坐标原点, .
. 的大小(结果用反三角函数值表示);
的大小(结果用反三角函数值表示); 为
为 轴上一点,求
轴上一点,求 的最大值及取得最大值时点
的最大值及取得最大值时点 与
与 的夹角为120°,且
的夹角为120°,且 ,则
,则 ______________
______________