题目内容
已知向量 ,
, ,且
,且 .
.
(1)求点 的轨迹
的轨迹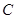 的方程;
的方程;
(2)设曲线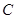 与直线
与直线 相交于不同的两点
相交于不同的两点 ,又点
,又点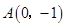 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围.
(1) .(2)当
.(2)当 时,m的取值范围是
时,m的取值范围是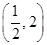 ,当
,当 时,m的取值范围是
时,m的取值范围是 .
.
解析试题分析:(1)由题意得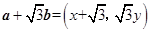 ,
,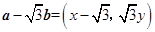 ,
, ,计算并化简得
,计算并化简得 .
.
(2)由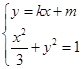 得
得 ,
,
由于直线与椭圆有两个不同的交点,∴ ,即
,即 .
.
讨论当 时,得所求的
时,得所求的 的取值范围是
的取值范围是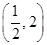 ;
;
当 时,得m的取值范围是
时,得m的取值范围是 .
.
(1)由题意得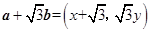 ,
,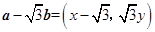 ,
,
∵ ,∴
,∴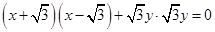 ,
,
化简得 ,∴
,∴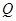 点的轨迹
点的轨迹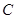 的方程为
的方程为 . 4分
. 4分
(2)由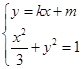 得
得 ,
,
由于直线与椭圆有两个不同的交点,∴ ,即
,即 .① 6分
.① 6分
(i)当 时,设弦
时,设弦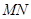 的中点为
的中点为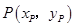 ,
,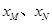 分别为点
分别为点 的横坐标,则
的横坐标,则 ,
,
从而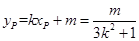 ,
,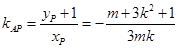 , 8分
, 8分
又 ,∴
,∴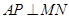 .
.
则 ,即
,即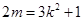 , ②
, ②
将②代入①得 ,解得
,解得 ,由②得
,由②得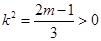 ,解得
,解得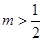 ,
,
故所求的 的取值范围是
的取值范围是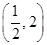 . 10分
. 10分
(ii)当 时,
时, ,∴
,∴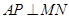 ,
, ,
,
解得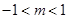 . 12分
. 12分
综上,当 时,m的取值范围是
时,m的取值范围是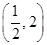 ,
,
当 时,m的取值范围是
时,m的取值范围是 . 13分
. 13分
考点:平面向量的数量积,椭圆方程,直线与圆锥曲线的位置关系.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 =(1,2),
=(1,2), =(-2,n) (n>1),
=(-2,n) (n>1), 与
与 ·
· =
=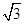 |
| |2,求角A,B,C的大小.
|2,求角A,B,C的大小.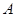 、
、 、
、 、
、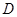 的坐标分别为
的坐标分别为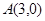 、
、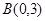 、
、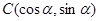 、
、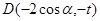 ,
,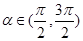
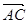 |=|
|=|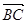 |,求角
|,求角 的值;
的值; ,求
,求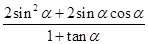 的值.
的值.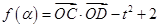 在定义域
在定义域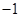 ,求
,求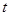 的值.
的值. (a>b>0)经过点M(
(a>b>0)经过点M( ,1),离心率为
,1),离心率为 .
. ,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由.
,试问直线AB是否恒过定点,若恒过定点,请给出证明,并求出该定点的坐标;若不过,请说明理由. =
= ,
, =
= ,若存在非零实数k,t使得
,若存在非零实数k,t使得 ,
, ,且
,且 ⊥
⊥ ,试求:
,试求: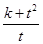 的最小值.
的最小值. =a,
=a, =b,求△ABC的面积.
=b,求△ABC的面积. 与
与 共线,设函数
共线,设函数 .
. 的周期及最大值;
的周期及最大值; ,边 BC=
,边 BC= ,
, ,求 △ABC 的面积.
,求 △ABC 的面积.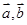 的夹角为120°,当
的夹角为120°,当 取得最小值时
取得最小值时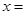 .
.