题目内容
设函数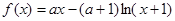 ,其中
,其中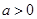
(1)求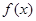 的单调区间;
的单调区间;
(2)当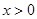 时,证明不等式:
时,证明不等式: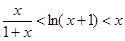 ;
;
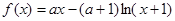 ,其中
,其中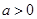
(1)求
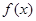 的单调区间;
的单调区间;(2)当
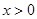 时,证明不等式:
时,证明不等式: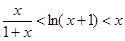 ;
;解:(1)由已知得函数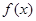 的定义域为
的定义域为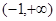 ,且
,且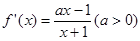 ,
,
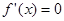 ,解得
,解得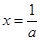
当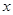 变化时,
变化时,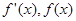 的变化情况如下表:
的变化情况如下表:
由上表可知,当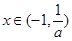 时,
时,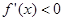 ,函数
,函数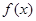 在
在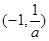 内单调递减,
内单调递减,
当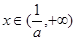 时,
时,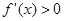 ,函数
,函数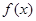 在
在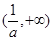 内单调递增,
内单调递增,
所以,函数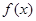 的单调减区间是
的单调减区间是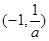 ,函数
,函数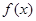 的单调增区间是
的单调增区间是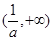
(2)设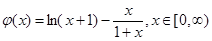
对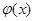 求导,得:
求导,得: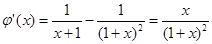
当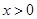 时,
时,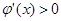 ,所以
,所以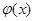 在
在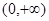 内是增函数。所以
内是增函数。所以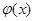 在
在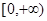 上是增函数。
上是增函数。
当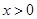 时,
时,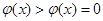 ,即
,即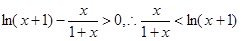
同理可证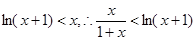 <x
<x
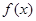 的定义域为
的定义域为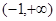 ,且
,且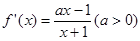 ,
,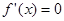 ,解得
,解得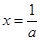
当
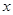 变化时,
变化时,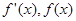 的变化情况如下表:
的变化情况如下表: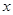 | 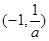 | 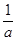 | 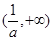 |
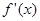 | - | 0 | + |
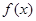 | ↘ | 极小值 | ↗ |
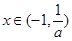 时,
时,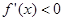 ,函数
,函数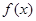 在
在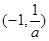 内单调递减,
内单调递减,当
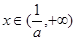 时,
时,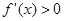 ,函数
,函数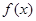 在
在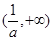 内单调递增,
内单调递增,所以,函数
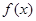 的单调减区间是
的单调减区间是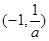 ,函数
,函数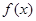 的单调增区间是
的单调增区间是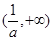
(2)设
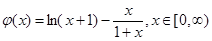
对
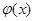 求导,得:
求导,得: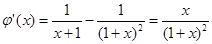
当
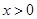 时,
时,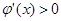 ,所以
,所以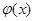 在
在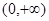 内是增函数。所以
内是增函数。所以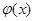 在
在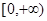 上是增函数。
上是增函数。当
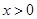 时,
时,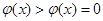 ,即
,即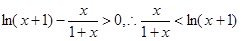
同理可证
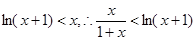 <x
<x略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
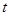 秒后的位移是
秒后的位移是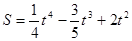 ,那么速度为零的时刻是_____________
,那么速度为零的时刻是_____________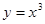 在点
在点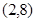 处的切线方程为( ).
处的切线方程为( ).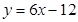
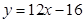
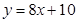
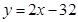
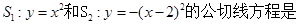 .
.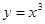 过点(2, 8)的切线方程;
过点(2, 8)的切线方程;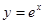 过点(0,0)的切线方程。
过点(0,0)的切线方程。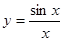 的导数为________.
的导数为________.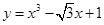 在点
在点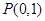 处的切线的倾斜角为( )
处的切线的倾斜角为( ) 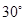
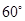
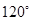
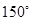
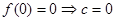 ,
,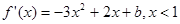 则
则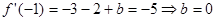 (4分)
(4分)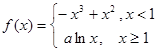 ,则
,则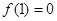
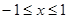 时,
时,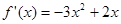 ,令
,令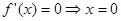 或
或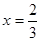
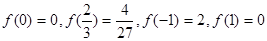 ,
,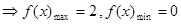
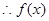 在
在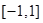 上的值域为
上的值域为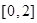 (7分)
(7分)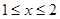 时, a.若
时, a.若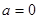 ,则
,则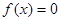
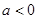 ,则
,则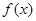 在
在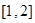 上是单调减的
上是单调减的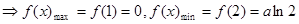
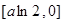
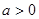 则
则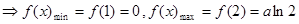
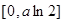 (9分)
(9分)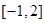 的值域为
的值域为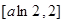 (10分)
(10分) 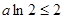
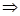
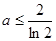 时,
时,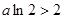
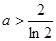 时,
时,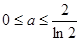 时,
时, 则
则
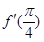 的值为____________.
的值为____________.