题目内容
方程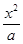 +
+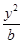 =1(
=1(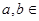 {1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
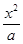 +
+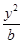 =1(
=1(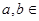 {1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .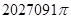 ,
,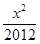 +
+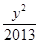 =1和
=1和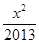 +
+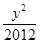 =1
=1试题分析:由公式
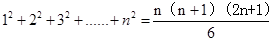 ,所有圆面积的和等于
,所有圆面积的和等于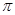 (
(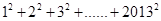 )=
)=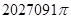 ;
;椭圆的离心率最小,即a,b最为接近,所以离心率最小的椭圆方程为
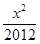 +
+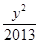 =1和
=1和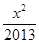 +
+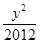 =1。
=1。点评:中档题,对于数列的求和公式
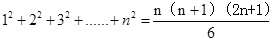 ,记忆清楚则题目不难,否则,推导公式要从头做起。
,记忆清楚则题目不难,否则,推导公式要从头做起。
练习册系列答案
相关题目
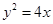 上任意一点
上任意一点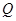 ,点
,点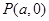 都满足
都满足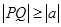 ,则
,则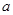 的取值范围是____ .
的取值范围是____ .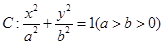 的离心率为
的离心率为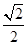 ,
,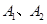 是椭圆的左右顶点,
是椭圆的左右顶点,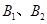 是椭圆的上下顶点,四边形
是椭圆的上下顶点,四边形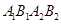 的面积为
的面积为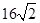 .
.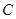 的方程;
的方程;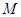 过
过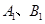 两点.当圆心
两点.当圆心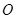 的距离最小时,求圆
的距离最小时,求圆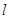 的斜率为2且过抛物线
的斜率为2且过抛物线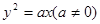 的焦点F,又与
的焦点F,又与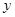 轴交于点A,
轴交于点A,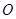 为坐标原点,若
为坐标原点,若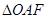 的面积为4,则抛物线的方程为:
的面积为4,则抛物线的方程为: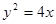
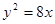
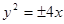
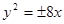
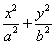 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为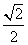 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(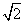 +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 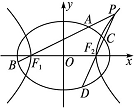
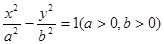 的左右焦点为
的左右焦点为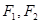 ,P为双曲线右支上
,P为双曲线右支上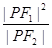 的最小值为8a,则双曲线的离心率的取值范围是 。
的最小值为8a,则双曲线的离心率的取值范围是 。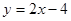 与抛物线
与抛物线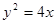 交于
交于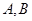 两点.
两点.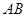 的长;(2)若抛物线
的长;(2)若抛物线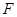 ,求
,求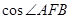 的值.
的值.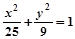 (y≠0)
(y≠0)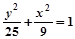 (y≠0)
(y≠0)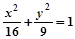 (y≠0)
(y≠0)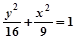 (y≠0)
(y≠0)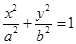 (a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )
(a>b>0)的两焦点为F1、F2,若椭圆上存在一点Q,使∠F1QF2=120º,椭圆离心率e的取值范围为( )