题目内容
对于抛物线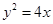 上任意一点
上任意一点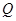 ,点
,点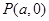 都满足
都满足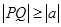 ,则
,则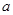 的取值范围是____ .
的取值范围是____ .
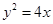 上任意一点
上任意一点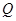 ,点
,点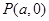 都满足
都满足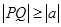 ,则
,则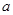 的取值范围是____ .
的取值范围是____ .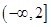
试题分析:解:设Q(
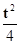 ,t),由|PQ|≥|a|得 (
,t),由|PQ|≥|a|得 (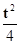 -a)2+t2≥a2,t2(t2+16-8a)≥0, t2+16-8a≥0,故t2≥8a-16恒成立,则8a-16≤0,a≤2,故a的取值范围是 (-∞,2],故答案为:(-∞,2].
-a)2+t2≥a2,t2(t2+16-8a)≥0, t2+16-8a≥0,故t2≥8a-16恒成立,则8a-16≤0,a≤2,故a的取值范围是 (-∞,2],故答案为:(-∞,2].点评:本题考查抛物线的标准方程,以及简单性质的应用,函数的恒成立问题,得到t2≥8a-16恒成立,是解题的关键

练习册系列答案
相关题目
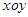 中,直线
中,直线 的参数方程为
的参数方程为 (t 为参数)。在极坐标系(与直角坐标系
(t 为参数)。在极坐标系(与直角坐标系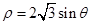 。
。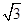 ),求|PA|+|PB|.
),求|PA|+|PB|. 上的任意一点
上的任意一点 (除短轴端点除外)与短轴两个端点
(除短轴端点除外)与短轴两个端点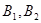 的连线交
的连线交 轴于点
轴于点 和
和 ,则
,则 的最小值是
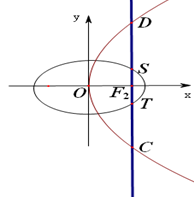
的最小值是 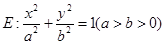 的右焦点
的右焦点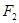 与抛物线
与抛物线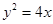 的焦点重合,过
的焦点重合,过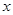 轴垂直的直线与椭圆交于
轴垂直的直线与椭圆交于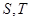 ,而与抛物线交于
,而与抛物线交于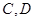 两点,且
两点,且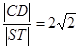 .
.
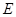 的方程;
的方程;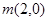 的直线与椭圆
的直线与椭圆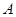 和
和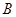 ,
,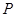 为椭圆
为椭圆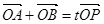 (
(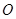 为坐标原点),求实数
为坐标原点),求实数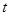 的取值范围.
的取值范围.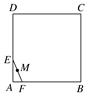
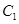 :
: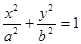 与双曲线
与双曲线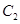 :
: 有相同的焦点
有相同的焦点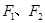 ,
,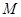 是椭圆
是椭圆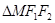 的周长为
的周长为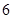 ,求椭圆
,求椭圆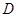 ”的方程为
”的方程为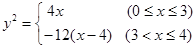 .设“盾圆
.设“盾圆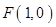 的距离为
的距离为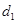 ,
,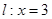 的距离为
的距离为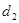 ,求证:
,求证: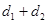 为定值;
为定值;
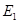 :
: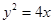 (
(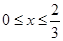 )与第(1)小题椭圆弧
)与第(1)小题椭圆弧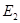 :
: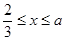 )所合成的封闭曲线为“盾圆
)所合成的封闭曲线为“盾圆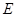 ”.设过点
”.设过点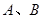 两点,
两点,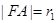 ,
,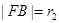 且
且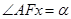 (
(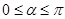 ),试用
),试用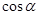 表示
表示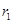 ;并求
;并求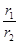 的取值范围.
的取值范围. .
.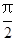 ),判断点P与直线L的位置关系;
),判断点P与直线L的位置关系;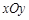 中,一直角三角形
中,一直角三角形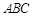 ,
,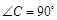 ,B、D在
,B、D在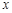 轴上且关于原点
轴上且关于原点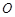 对称,
对称,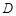 在边
在边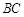 上,BD=3DC,△ABC的周长为12.若一双曲线
上,BD=3DC,△ABC的周长为12.若一双曲线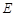 以B、C为焦点,且经过A、D两点.
以B、C为焦点,且经过A、D两点.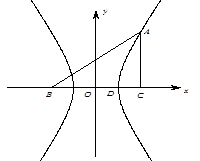
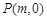 (
(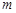 为非零常数)的直线
为非零常数)的直线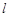 与双曲线
与双曲线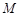 、
、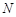 ,且
,且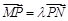 ,问在
,问在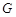 ,使
,使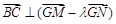 ?若存在,求出所有这样定点
?若存在,求出所有这样定点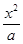 +
+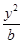 =1(
=1(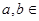 {1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .
{1,2,3,4,…,2013})的曲线中,所有圆面积的和等于 ,离心率最小的椭圆方程为 .