Question

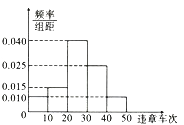
【题目】某水产品经销商销售某种鲜鱼，售价为每公斤元，成本为每公斤元.销售宗旨是当天进货当天销售.如果当天卖不出去，未售出的全部降价处理完，平均每公斤损失元.根据以往的销售情况，按，，，，进行分组，得到如图所示的频率分布直方图.

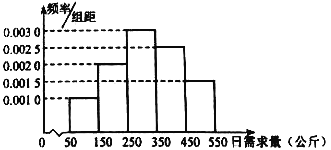
（1）求未来连续三天内，该经销商有连续两天该种鲜鱼的日销售量不低于公斤，而另一天日销售量低于公斤的概率；

（2）在频率分布直方图的需求量分组中，以各组区间的中点值代表该组的各个值.

（i）求日需求量的分布列；

（ii）该经销商计划每日进货公斤或公斤，以每日利润的数学期望值为决策依据，他应该选择每日进货公斤还是公斤？

Answer 1

【答案】(1)0.192(2) （ⅰ）见解析（ⅱ）该经销商应该选择每日进货400公斤

【解析】试题分析：（1）根据频率分布直方图得到不低于350公斤的概率为0.4，有连续两天该种鲜鱼的日销售量不低于公斤，而另一天日销售量低于公斤的概率即分两种情况按照概率相乘计算即可；（2）（i）X可取100，200，300，400，500，根据图得到对应的长方形的概率值，（ii）根据题意求出进货量为300，400时的利润均值，选择较高的即可.

解析;’

（Ⅰ）由频率分布直方图可知，

日销售量不低于350公斤的概率为(0.0025＋0.0015)×100＝0.4，

则未来连续三天内，有连续两天的日销售量不低于350公斤，而另一天日销售量低于350公斤的概率P＝0.4×0.4×(1－0.4)＋(1－0.4)×0.4×0.4＝0.192．

（Ⅱ）（ⅰ）X可取100，200，300，400，500，

P(X＝100)＝0.0010×10＝0.1； P(X＝200)＝0.0020×10＝0.2；

P(X＝300)＝0.0030×10＝0.3； P(X＝400)＝0.0025×10＝0.25；

P(X＝500)＝0.0015×10＝0.15；

所以X的分布列为：

（ⅱ）当每日进货300公斤时，利润Y1可取－100，700，1500，

此时Y1的分布列为：

此时利润的期望值E(Y1)＝－100×0.1＋700×0.2＋1500×0.7＝1180；

当每日进货400公斤时，利润Y2可取－400，400，1200，2000，

此时Y2的分布列为：

此时利润的期望值E(Y2)＝－400×0.1＋400×0.2＋1200×0.3＋2000×0.4＝1200；

因为E(Y1)＜E(Y2)，

所以该经销商应该选择每日进货400公斤．