题目内容
【题目】2017年8月20日起，市交警支队全面启动路口秩序环境综合治理，重点整治机动车不礼让斑马线和行人的行为，经过一段时间的治理，从市交警队数据库中调取了20个路口近三个月的车辆违章数据，经统计得如图所示的频率分布直方图，统计数据中凡违章车次超过30次的设为“重点关注路口”.
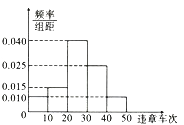
(1)现从“重点关注路口”中随机抽取两个路口安排交警去执勤，求抽出来的路口的违章车次一个在
，一个在
中的概率；
(2)现从支队派遣5位交警，每人选择一个路口执勤，每个路口至多1人，违章车次在的路口必须有交警去，违章车次在
的不需要交警过去，设去“重点关注路口”的交警人数为
，求的分布列及数学期望.
【答案】(1) 
(2) 
【解析】试题分析：（1）根据频率分布直方图, 违章车次在
的路口有5, 在
中的路口有2,利用古典概型公式易得结果；（2）由题知随机变量
可取值2，3，4，5，计算相应的概率值，得到分布列及相应的期望值.
试题解析：
（Ⅰ）根据频率分布直方图，违章车次在的路口有
，
在中的路口有
，
设抽出来的路口违章车次一个在，一个在的事件为
，
则
．
（Ⅱ）由题知随机变量可取值2，3，4，5，
， 
，
， 
．
．
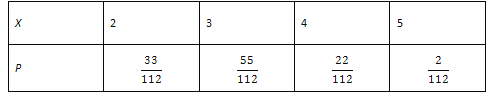
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
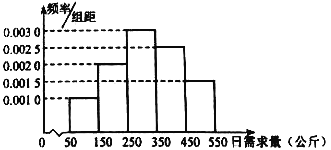
【题目】从某工厂的一个车间抽取某种产品50件，产品尺寸（单位：
）落在各个小组的频数分布如下表：
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
（1）根据频数分布表，求该产品尺寸落在
的概率；
（2）求这50件产品尺寸的样本平均数
.（同一组中的数据用该组区间的中点值作代表）；
（3）根据频数分布对应的直方图，可以认为这种产品尺寸
服从正态分布
，其中
近似为样本平均值，
近似为样本方差
，经计算得
.利用该正态分布，求
.
附：（1）若随机变量服从正态分布，则
，
；
（2）
.
