题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)若![]() 在定义域上是增函数,求
在定义域上是增函数,求![]() 的取值范围;
的取值范围;
(2)若存在![]() ,使得
,使得![]() ,求
,求![]() 的值,并说明理由.
的值,并说明理由.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)问题等价于![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,
,![]() ,进而求最值即可.
,进而求最值即可.
(2)取![]() ,易得
,易得![]() ,所以存在整数
,所以存在整数![]() ,当
,当![]() 时,
时,![]() ,令
,令![]() ,令
,令![]() ,证明
,证明![]() 时不等式成立即可.
时不等式成立即可.
试题解析:
(1)因为![]() 在定义域上为增函数.
在定义域上为增函数.
所以![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立.
上恒成立.
令![]() ,
,![]() ,则
,则![]() ,
,
所以![]() 在
在![]() 上为减函数,故
上为减函数,故![]() ,所以
,所以![]() .
.
故![]() 的取值范围为
的取值范围为![]() .
.
(2)因为![]() ,
,
取![]() ,得
,得![]() ,又
,又![]() ,所以
,所以![]() .
.
所以存在整数![]() ,当
,当![]() 时,
时,![]() .
.
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() .
.
![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:

所以![]() 时,
时,![]() 取到最小值,且最小值为
取到最小值,且最小值为![]() .
.
即![]() .
.
令![]() ,则
,则![]() ,
,
令![]() ,由
,由![]() ,得
,得![]() ,
,
所以当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
因此![]() ,从而
,从而![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() ,即
,即![]() .
.
综上,![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
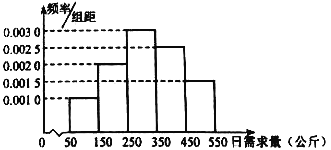
【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这50件产品尺寸的样本平均数![]() .(同一组中的数据用该组区间的中点值作代表);
.(同一组中的数据用该组区间的中点值作代表);
(3)根据频数分布对应的直方图,可以认为这种产品尺寸![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为样本平均值
近似为样本平均值![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() .利用该正态分布,求
.利用该正态分布,求![]() .
.
附:(1)若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则
![]() ,
,![]() ;
;
(2)![]() .
.
【题目】交管部门为宣传新交规举办交通知识问答活动,随机对该市![]() 岁的人群抽样了
岁的人群抽样了![]() 人,回答问题统计结果如图表所示:
人,回答问题统计结果如图表所示:
分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | |
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
第 |
|
|
|
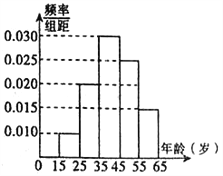
(1)分别求出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)从第![]() ,
,![]() ,
,![]() 组回答正确的人中用分层抽样方法抽取
组回答正确的人中用分层抽样方法抽取![]() 人,则第
人,则第![]() ,
,![]() ,
,![]() 组每组应各抽取多少人?
组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的![]() 人中随机抽取
人中随机抽取![]() 人颁发幸运奖,求:所抽取的
人颁发幸运奖,求:所抽取的![]() 人中至少有一个第
人中至少有一个第![]() 组的人的概率.
组的人的概率.