题目内容
【题目】设a,b均大于0,且 ![]() +
+ ![]() =1.求证:对于每个n∈N* , 都有(a+b)n﹣(an+bn)≥22n﹣2n+1 .
=1.求证:对于每个n∈N* , 都有(a+b)n﹣(an+bn)≥22n﹣2n+1 .
【答案】证明:由a,b均大于0,且 ![]() +
+ ![]() =1,
=1,
可得 ![]() 知
知 ![]() ,
,
由二项式定理,得 ![]()
= ![]()
![]() .
.
则原不等式成立.
【解析】运用二元均值不等式可得 ![]() ≥2,再由二项式定理,化简整理可得(a+b)n﹣(an+bn)
≥2,再由二项式定理,化简整理可得(a+b)n﹣(an+bn)
= ![]() ,再由均值不等式即可得证.
,再由均值不等式即可得证.
【考点精析】解答此题的关键在于理解不等式的证明的相关知识,掌握不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等,以及对平均值不等式的理解,了解平均不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取
时取![]() 号即调和平均
号即调和平均![]() 几何平均
几何平均![]() 算术平均
算术平均![]() 平方平均)
平方平均)
.

练习册系列答案
相关题目
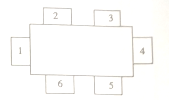
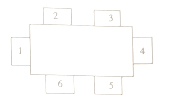
【题目】在一次体育兴趣小组的聚会中,要安排![]() 人的座位,使他们在如图所示的
人的座位,使他们在如图所示的![]() 个椅子中就坐,且相邻座位(如
个椅子中就坐,且相邻座位(如![]() 与
与![]() ,
, ![]() 与
与![]() )上的人要有共同的体育兴趣爱好.现已知这
)上的人要有共同的体育兴趣爱好.现已知这![]() 人的体育兴趣爱好如下表所示,且小林坐在
人的体育兴趣爱好如下表所示,且小林坐在![]() 号位置上,则
号位置上,则![]() 号位置上坐的是( )
号位置上坐的是( )
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |
A. 小方 B. 小张 C. 小周 D. 小马