Question

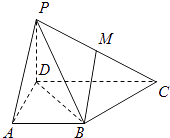
【题目】如图，三棱柱ABC﹣A1B1C1中，AB=AC=AA1=BC1=2，∠AA1C1=60°，平面ABC1⊥平面AA1C1C，AC1与A1C相交于点D．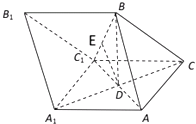

（1）求证：BD⊥A1C；
（2）若E在棱BC1上，且满足DE∥面ABC，求三棱锥E﹣ACC1的体积．

Answer 1

【答案】
（1）证明：侧面AA1C1C是菱形，D是AC1的中点，∵BA=BC1，∴BD⊥AC1，

∵平面ABC1⊥平面AA1C1C，且BD平面ABC1，平面ABC1∩平面AA1C1C=AC1，

∴BD⊥平面AA1C1C，则BD⊥A1C

（2）解：∵DE∥面ABC，DE面ABC1，面ABC1∩面ABC=AB，∴DE∥AB，

∵点D为AC1的中点，∴点E为BC1的中点，

∵AA1=AC=2，∠AA1C1=60°，∴AC1=2，∵AB=BC1=2，

∴△ABC1为正三角形，则 ，

∴点E到面ACC1的距离等于 ，

∴ ．

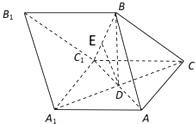
【解析】（1）由已知，可得BD⊥AC1 ， 结合平面ABC1⊥平面AA1C1C，利用面面垂直的性质可得BD⊥A1C；（2）由题意可得△ABC1为正三角形，求得 ，再由E为BC1的中点求得E到平面ACC1的距离，求出△ACC1的面积，代入棱锥体积公式得答案．