题目内容
9.已知$\overrightarrow{a}$=(cosα,sinα),$\overrightarrow{b}$=(cosβ,sinβ),|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\frac{2\sqrt{5}}{5}$,若0<α<$\frac{π}{2}$,-$\frac{π}{2}$<β<0,且sinβ=-$\frac{5}{13}$,求sinα.分析 由条件|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\frac{2\sqrt{5}}{5}$,求得cos(α-β)的值,可得sin(α-β)的值;再根据sinβ=-$\frac{5}{13}$,求得cosβ 的值,从而利用两角和的正弦公式求得sinα=sin[(α-β)+β]的值.
解答 解:由题意可得$\overrightarrow{a}$-$\overrightarrow{b}$=(cosα-cosβ,sinα-sinβ),|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\frac{2\sqrt{5}}{5}$=$\sqrt{{(cosα-cosβ)}^{2}{+(sinα-sinβ)}^{2}}$=$\sqrt{2-2cos(α-β)}$,
∴cos(α-β)=$\frac{3}{5}$.
∵0<α<$\frac{π}{2}$,-$\frac{π}{2}$<β<0,且sinβ=-$\frac{5}{13}$,∴cosβ=$\sqrt{{1-sin}^{2}β}$=$\frac{12}{13}$,α-β∈0,π),∴sin(α-β)=$\sqrt{{1-cos}^{2}(α-β)}$=$\frac{4}{5}$,
∴sinα=sin[(α-β)+β]=sin(α-β)cosβ+cos(α-β)sinβ=$\frac{4}{5}×\frac{12}{13}$+$\frac{3}{5}×(-\frac{5}{13})$=$\frac{33}{65}$.
点评 本题主要考查两个向量的数量积的运算,同角三角函数的基本关系,两角差的三角公式的应用,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
4.若a=${log}_{\sqrt{2}}$$\frac{1}{\sqrt{3}}$,b=${log}_{\sqrt{2}}\frac{1}{\sqrt{2}}$,c=-2,则a、b、c的大小关系是( )
| A. | a>b>c | B. | b>c>a | C. | b>a>c | D. | c>b>a |
19.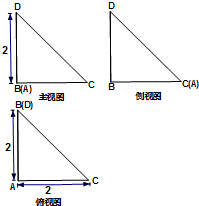 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
 如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )
如图所示是三棱锥D-ABC的三视图,若在三棱锥的直观图中,点O为线段BC的中点,则异面直线DC与AB所成角的余弦值等于( )| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,且AC=AA1.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,AB⊥AC,且AC=AA1.