题目内容
2.已知集合M={(x,y)|y=0},N={(x,y)|y=ax2+2bx+c,a≠0},L={(x,y)|y=dx2+2ex+f,d≠0},且a,b,c,d,e,f∈R,2be=ac+df.(1)求M∩N为单元素集的条件;
(2)求证:(M∩N)∪(M∩L)≠∅.
分析 (1)M∩N为单元素集即直线y=0与函数y=ax2+2bx+c的图象只有一个交点,进而得到答案;
(2)若(M∩N)∪(M∩L)=∅.则直线y=0与函数y=ax2+2bx+c和y=dx2+2ex+f的图象均无交点,则4b2-4ac<0且4e2-4df<0,结合已知由不等式的性质和基本不等式,得到矛盾,进而得到(M∩N)∪(M∩L)≠∅.
解答 解:(1)∵集合M={(x,y)|y=0},N={(x,y)|y=ax2+2bx+c,a≠0},
若M∩N为单元素集,
即直线y=0与函数y=ax2+2bx+c的图象只有一个交点,
即函数y=ax2+2bx+c的顶点的纵坐标$\frac{4ac-4{b}^{2}}{4a}$=0,
即b2=ac,
证明:(2)若(M∩N)∪(M∩L)=∅.
则直线y=0与函数y=ax2+2bx+c和y=dx2+2ex+f的图象均无交点,
则4b2-4ac<0且4e2-4df<0,
即b2<ac且e2<df,
则b2+e2<ac+df=2be,
这与b2+e2≥2be矛盾.
故假设不成立,
故(M∩N)∪(M∩L)≠∅.
点评 本题考查的知识点是集合的交集,并集和补集运算,二次函数的图象和性质,是函数与集合的综合应用,难度中档.

练习册系列答案
相关题目
13.已知函数f(x)在R上是增函数,若a+b>0,则( )
| A. | f(a)+f(b)>f(-a)+f(-b) | B. | f(a)+f(b)>f(-a)-f(-b) | C. | f(a)+f(-a)>f(b)-f(-b) | D. | f(a)+f(-a)>f(b)-f(-b) |
14.已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1},B⊆A,则m的取值范围是( )
| A. | m<2 | B. | m<3 | C. | 2<m≤3 | D. | m≤3 |
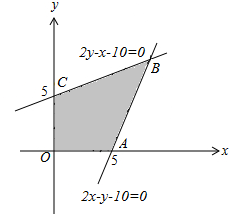 如图.已知线性规划的可行域是由直线x=0,y=0,2y-x-10=0和2x-y-10=0围成的四边形.若点B是使目标函数z=ax+y取最大值的点.求a的取值范围.
如图.已知线性规划的可行域是由直线x=0,y=0,2y-x-10=0和2x-y-10=0围成的四边形.若点B是使目标函数z=ax+y取最大值的点.求a的取值范围.